2. В качестве предпосылки мне необходимо средство, которое само по себе представляет определенный интерес - нечто вроде упрощенного способа представления хорошо знакомого теперь анализа потребительского спроса. Для общей теории (равновесия или оптимума) это представление хуже, чем представление с помощью кривой безразличия; но для частичного анализа оно значительно более удобно. С педагогической точки зрения оно имеет бесспорное преимущество, заключающееся в том, что сводит к минимуму чисто геометрические трудности. Интерес студента, таким образом, концентрируется на экономических проблемах, а не на геометрических свойствах, интерес к которым иногда конкурирует с интересом к экономическим вопросам.
Первый шаг анализа заключается в переопределении "кривой предельной полезности" Маршалла таким образом, чтобы учесть эффекты дохода и исключить какие бы то ни было ссылки на "измеримую" полезность. Предположим, что мы рассматриваем потребителя с заданным денежным доходом, который столкнулся с заданными рыночными ценами n-1 товаров. Если бы ему пришлось ограничить свои покупки этими n-1 товарами, он бы разложил свои расходы так-то и так-то. Теперь предположим, что появился другой товар; положим, что сначала предлагается только одна единица этого n-го товара. Захочет ли он приобретать эту единицу? Ясно, что это будет зависеть от цены. Если цена слишком высока, он не станет покупать; если она очень низкая, он с готовностью его приобретет. Найдется некая промежуточная цена, между высокими ценами, при которых он не будет покупать, и низкими, при которых он захочет купить,-цена, при которой он будет на грани приобретения. Назовем эту цену его предельной оценкой единицы товара. (Очевидно, что это то же самое, что и "предельная полезность в денежном выражении" Маршалла).
При заданных потребностях, заданном доходе и заданных ценах на другие товары предельная оценка первой единицы товара - это совершенно определенная величина. Если фактическая цена меньше предельной оценки, товар будет куплен; если она больше, товар не купят. Но (и это то, что традиционное представление не выявляет столь ясно) предельная оценка второй единицы товара не обязательно определяется тем же самым способом. Предельная оценка второй единицы зависит от цены, уплаченной за первую. Если первая единица была приобретена очень дешево, потребитель окажется в лучшем положении (у него будет больше денег), чем если бы ему пришлось уплатить бешеную цену за первую единицу товара.
 |
 |
С другой стороны, когда цена, которую нужно заплатить за первую единицу, задана, предельная оценка второй определена. Когда фактическая цена Второй задана, предельная оценка третьей определена; и т. д. Таким образом, если мы предположим, что товар имеет заданную рыночную цену, предельные оценки всех единиц определены. Но предельные оценки зависят от заданной рыночной цены.
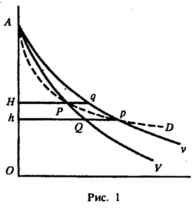
Теперь мы можем вычертить эту ситуацию на графике уже знакомого нам вида (рис. 1), где количества - на горизонтальной оси, а цены - на вертикальной. Если ОН - заданная рыночная цена, действительная для любого количества единиц, AV будет определенной кривой предельной оценки. До тех пор, пока предельная оценка единицы товара больше цены ОН, эту единицу будут покупать. Приобретенное количество будет тогда равно HP, где Р- точка пересечения AV с горизонтальной линией, проходящей через H.
Нисходящий наклон кривой предельной оценки в точке Р - необходимое условие стабильности. Мы можем сохранить договоренность чертить ее всюду нисходящей, хотя в действительности ничто не исключает возможности того, что она может немного подниматься, прежде чем начнет опускаться.
Теперь, что происходит, если цена меняется? Положим, что рыночная цена (все еще действительная для любого количества единиц) падает с ОН до Oh. Это никак не изменит предельную оценку первой единицы, но может внести изменение в предельную оценку последующих единиц, поскольку, когда потребитель теперь приходит, чтобы купить эти единицы, у него есть немного больше денег, которые он может потратить. Это эффект дохода; увеличение покупательной способности (при прочих равных условиях) обычно делает потребителя более склонным к приобретению конкретной по счету единицы товара - таким образом, оно повышает ее предельную оценку. Но иногда оно может уменьшить его желание покупать (случай неполноценного блага).
За исключением случая неполноценного блага, падение цены имеет, таким образом, тенденцию несколько поднимать кривую предельной оценки; она будет поворачиваться вокруг своего левого конца, поскольку на предельную оценку первой единицы повлиять нельзя. Я изобразил новое положение как Av (рис. 1), для удобства значительно преувеличив возможное смещение. Точка равновесия при цене Oh, таким образом, находится в р, где AV пересекает горизонтальную линию, проходящую через h. Таким образом, падение цены перемещает точку равновесия из Р в р; происходит движение вдоль кривой AV (или Av), a также смещение от одной кривой к другой.
Поскольку движение вдоль кривой предельной оценки - не то же самое, что движение вдоль кривой безразличия (потребитель оказывается в лучшем положении по мере продвижения вниз по кривой предельной оценки), это различие не совсем то же самое, что различие между эффектами замены и дохода, приведенное в работе Value and Capital.
Но это различие для большинства случаев, видимо, не имеет большого значения.3 Лишь в редких случаях мы ошибемся, если отождествим движение вдоль кривой предельной оценки с эффектом замены, а движение от одной кривой к другой - с эффектом дохода.
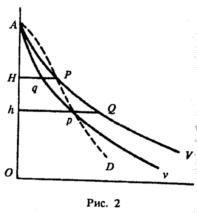
Основные утверждения об этих двух эффектах вытекают сразу же из графика. В обычном случае (рис. 1) оба эффекта действуют в одном и том же направлении; но в случае неполноценного блага (рис. 2) они могут действовать в противоположных направлениях.
Кривая потребительского спроса получается (безо всяких манипуляций), если отмечать положение Р по мере изменения цены. Поскольку при цене ОА будет приобретена одна единица, кривая спроса начнется из точки А, как и все кривые предельной оценки. (На каждом рисунке она показана пунктирной кривой AD). Очевидно, как это и должно быть, что кривая спроса для обычного случая более эластична, чем кривые предельной оценки, которые она пересекает; но в случае неполноценного блага она менее эластична.
 |
3. Мы увидели, как различить эффекты замены и дохода адекватным, как кажется, способом, не используя ничего, кроме Маршаллианской геометрии. Можно ли использовать тот же способ построения в случае излишка потребителя?
К данному вопросу надо подходить с осторожностью. Из наших предыдущих изысканий4 стало ясно, что, когда мы учитываем эффекты дохода, оказывается, что излишек потребителя - это не одно понятие, а несколько. Нам придется рассмотреть эти разные определения по очереди. Мы увидим, что все их можно различить на нашем графике.
Начнем с определения приращения излишка потребителя, которое я ввел в работе Value and Capital и назвал "Компенсирующей Вариацией". Цена падает с ОН до Oh; мы спрашиваем, что такое "потеря дохода", которая компенсировала бы воздействие цены, оставляя благосостояние потребителя тем же, что и прежде. То есть мы пытаемся найти такую потерю дохода, при которой, если бы она произошла при цене Oh, потребитель остался бы в столь же хорошем положении, в каком он находится со своим фактическим доходом при цене ОН. Ее можно определить следующим образом.
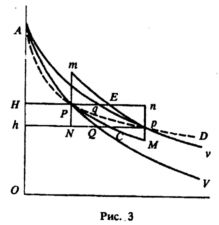
Предположим, что последовательные единицы товара поставляются потребителю по следующему плану. Прежде всего ему дают возможность приобрести HP единиц по цене ОН. По этой цене больше единиц он бы не приобрел, поэтому для того чтобы побудить его приобрести следующую единицу, цену снижают, но не более, чем это необходимо, чтобы побудить его приобрести следующую единицу. Затем, чтобы побудить его приобрести следующую единицу товара, цену снова снижают, но опять не более, чем это необходимо. И так далее, пока цена не опустится до Oh, после чего дальнейшее снижение не происходит.
При таком подходе будет пройден путь НРС (рис. 3). С должна находиться между Q и р, поскольку в точке С потребитель в лучшем положении, чем если бы его вынуждали приобретать дополнительные единицы товара по более высокой цене ОН (заметим, что он не делал бы этого, если бы не был подвергнут некоторой форме принуждения), но в худшем положении, чем если бы ему позволили приобрести все единицы по цене Oh. Кривая PC, следовательно, должна лежать между кривой предельной оценки PV кривой спроса Pp. Следовательно, С должна лежать между Q и р.
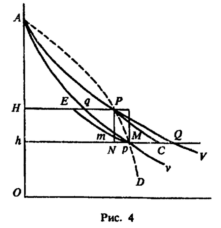 |
В случае неполноценного блага будет та же самая "промежуточность" (рис. 4); но в этом случае точка QCp будут расположены в обратном порядке.
Теперь рассмотрим положение потребителя в точке С, когда он пришел к ней этим особенным маршрутом. Он настолько же в хорошем положении, насколько был в Р, поскольку каждая последующая приобретенная единица не делала его положение ни лучше, ни хуже. Он может приобрести предельную единицу по цене Oh, но за каждую предыдущую единицу он заплатил избыточную цену сверх Oh, причем эти избыточные цены измеряются ординатами фигуры HPCh. Таким образом, он находится точно в таком же положении, как если бы цена все время была равна Oh, но он потерял бы в денежном доходе величину, равную площади данной фигуры. Следовательно, эта площадь HPCh является мерой Компенсирующей Вариации - величины дохода, который ему пришлось бы потерять, чтобы уравновесить выгоду, обусловленную падением цены.
Если бы вместо того, чтобы рассматривать падение цены с ОН до Oh, мы бы рассматривали повышение цены с Oh до ОН, мы получили бы другое выражение для компенсирующей вариации. Ибо компенсирующие вариации в этих двух направлениях не представляют одно и то же. Одна представляет потерю дохода, понесенную при цене Oh, другая - прирост дохода при цене ОН. Прирост и потеря равны, если они измерены "полезностью"; но они не равны в денежном выражении, поскольку ценность денег в товарном выражении в этих двух случаях различна. Таким образом, нам нужно отличать Компенсирующую Вариацию для движения цены вверх от Компенсирующей Вариации для движения цены вниз.
Как я отмечал ранее,5 величина Компенсирующей Вариации "вверх" продолжает интересовать нас даже тогда, когда фактическое изменение, которое мы анализируем, - это понижение, а не повышение. Ибо, когда мы рассматриваем падение цены, вариацию "вверх" можно определить как "прирост дохода, который, если бы происходил без падения цены, настолько же улучшил бы положение, насколько оно улучшается при падении цены без изменения денежного дохода". Именно по этой причине я назвал эту вторую меру "Эквивалентной Вариацией". Когда мы рассматриваем падение цены с ОН до Oh, - это Эквивалентная Вариация, но она становится Компенсирующей Вариацией, когда мы рассматриваем рост цены с Oh до ОН. Эти две "вариации" меняются местами, когда мы вместо снижения рассматриваем повышение цены. Эквивалентная Вариация становится Компенсирующей, а Компенсирующая становится Эквивалентной.
Эквивалентная Вариация (для падения цены) измеряется на рис. 3 следующим образом. Начиная с р, где hp единиц были приобретены по цене Oh, мы выясняем минимальные цены, которые потребитель затребовал бы для снижения потребления ниже этой точки на первую, вторую, третью..., единицы. Таким образом, мы прослеживаем кривую рЕ. В точке Е (на горизонтальной линии, проходящей через точку Н) ему точно также хорошо, как и в точке р; но оценка предельной сохраняемой единицы теперь стала ОН. Однако он приобрел НЕ единиц по общей стоимости, гораздо более низкой, чем если бы он уплатил за каждую единицу цену ОН. Разница в его чистом расходе, как результат данного конкретного способа приобретения, измеряется площадью HEph. Таким образом, он находится в таком же положении, как если бы он приобрел НЕ единиц по более высокой цене, но имел бы прирост дохода, равный этой площади. Таким образом, именно этой площадью измеряется Эквивалентная Вариация.
Мы увидели, что точка С должна лежать между Q и р; однако Е не находится между Р и q. Сравните положение потребителя в Е с тем положением, в котором он находился бы, если бы приобрел то же количество единиц, следуя кривой предельной оценки Apv. В точке Е ему столь же хорошо, как в точке р; но в точке, расположенной на Av вертикально под Е, он в менее желательном положении, чем в р (он улучшает свое положение по мере того, как спускается по кривой предельной оценки к точке р). Следовательно, его предельная оценка того же количества единиц должна быть ниже (за исключением случая неполноценного блага); поэтому, когда на рис. 3 мы поместили кривую рЕ выше pq, мы начертили ее правильно.
Таким образом, в случае эквивалентной вариации, q должна лежать между Р и Е; такое расположение сохраняется для случая неполноценного блага, но опять-таки точки PqE следуют в обратном порядке (рис. 4).
4. Другое преимущество аппарата, который я использую в данной работе, заключается в том, что он проливает немало света на вопрос, который поставил господин Хендерсон в своей статье, посвященной данной теме.6 Если мы вернемся к компенсирующей вариации, то заметим, что в точке С потребитель фактически покупает меньше товара, чем в р; он должен так поступать, если имеет место положительный эффект дохода, и этот эффект ощутим. Таким образом, компенсирующая вариация в том виде, как мы ее определили, не является мерой дополнительной цены, которую потребитель был бы согласен заплатить за дополнительные единицы товара, которые он получает, когда цена падает до Oh, а его доход не изменяется. Что измеряет компенсирующая вариация - так это изменение дохода, требующееся, чтобы служить противовесом падению цены, а не то изменение дохода, которое необходимо, чтобы уравновесить увеличение приобретаемого количества товара. Становится очевидным, что это не одно и то же.
Следовательно, мы должны отличать то, что я теперь могу назвать "компенсирующей вариацией по цене" (с которой мы имели дело до сих пор), от "компенсирующей вариации по количеству" (на которую мы теперь должны переключить свое внимание). Очень вероятно (как показал господин Хендерсон), что Маршалл главным образом имел в виду именно компенсирующую вариацию по количеству, а не компенсирующую вариацию по цене. Но очевидно, что он не потрудился различать эти две вариации.
Для того чтобы представить на нашем графике (рис, 3) компенсирующую вариацию по количеству, мы должны продолжить линию PC дальше (предполагая, что цена продолжает падать до размера, достаточного для стимулирования приобретения каждой дополнительной единицы). Мы должны продолжить ее до той точки, где она пересечет ординату р в точке М. В точке М потребитель столь же состоятелен, сколь был в точке Р, хотя и имеет такое же количество товара, как в точке р. Но по сравнению со своим положением в р, он потерял в доходе величину, равную компенсирующей вариации по цене HPCh, за вычетом треугольника СМр. Таким образом, именно эта разность определяет величину компенсирующей вариации по количеству.
Точно так же, как существует "количественная" вариация, соответствующая компенсирующей вариации по цене, должна существовать и "количественная" вариация, соответствующая эквивалентной мере. (Мы получим ее, если, например, вместо падения цены станем рассматривать рост). Для того чтобы измерить эквивалентную вариацию по количеству, мы должны таким же образом продолжить дальше кривую рЕ (предположив, что цена, продолжает расти в достаточной степени, чтобы стимулировать отказ от каждой дополнительной единицы) до тех пор, пока эта кривая не пересечет ординату Р в точке т. В точке m потребителю столь же хорошо, как и в р, хотя у него не больше единиц данного товара, чем в Р; но по сравнению с его положением в Р, его покупательная способность увеличилась на величину, равную эквивалентной вариации по цене HEph, плюс треугольник ЕmР. Таким образом, именно суммой этих площадей измеряется эквивалентная вариация по количеству.
Если мы проследим это доказательство по рис. 4, то заметим, что те же самые выводы справедливы и в случае неполноценного блага. По-прежнему верно то, что компенсирующая вариация по количеству меньше компенсирующей вариации по цене на треугольник СМр; и что эквивалентная по количеству превышает эквивалентную по цене на треугольник ЕmР.
5. Теперь, дав четыре определения Излишка Потребителя, посмотрим, какие выводы об арифметических соотношениях их величии можно сделать из нашего графика. Совершенно очевидно, что в наиболее, по-видимому, распространенном случае, когда эффект дохода положителен, но относительно мал, компенсирующая вариация по количеству, компенсирующая вариация по цене, эквивалентная вариация по цене, и эквивалентная вариация по количеству образуют возрастающую последовательность величин и будут лежать между "внутренним" и "внешним" прямоугольниками HPNh и Нnph. Но уже из рис. 4 видно, что эти неравенства будут выполняться не во всех случаях. Но можем ли мы сказать что-либо более определенное?
Можем, если ограничимся малым изменением цены, полагая, что H и h находятся очень близко друг к другу, ибо в этом случае можно легко установить различия между разными вариациями.
Если рассматриваемое нами изменение цены мало, мы получаем следующие упрощения. 1. Все кривые между Р и р (или соответствующими точками) можно рассматривать как прямые линии.2. Линии PQ и PC совпадают друг с другом, то же происходит и с pq и рЕ. Ибо разница между PQ и PC зависит от разницы в ценах только на предельные единицы. Таким Образом, если все расстояние между двумя кривыми оценки мало, хотя это и зависит от изменения цены всего приобретенного количества, расстояния QC и qE, которые зависят только от изменений цены предельных единиц, должны быть малыми величинами второго порядка.73. Подобным же образом разница между расстояниями Pq и Qp, каждое из которых - величина первого порядка, должна быть малой величиной второго порядка. Следовательно, PQpq можно рассматривать как параллелограмм, и он совпадает с РСрЕ, который, следовательно, также можно считать параллелограммом. Отсюда треугольники PNC и рnЕ можно считать равными; и как равные можно рассматривать треугольники РСр и рЕР.
Площадь треугольника PNC обозначим ½S; S неизбежно положительна, поскольку кривая PC должна проходить вниз вправо. Величина S зависит от величины эффекта замены. Мы только что доказали, что для малого изменения цены площадь треугольника рnЕ можно также принять за ½S.
Площадь треугольника РСр обозначим ½I; I зависит от эффекта дохода. Она положительна, если эффект дохода положителен (рис. 3), но отрицательна, если эффект дохода отрицателен (рис. 4). Только что для малого изменения цены мы доказали, что площадь треугольника рЕР можно принять за ½I.
Теперь о площади треугольника СМр, которым измеряется разница между компенсирующей вариацией по цене, и компенсирующей вариацией по количеству. Для малого изменения цены мы можем рассматривать РСМ (или на рис. 4 РМС) как прямую линию. Таким образом, треугольники PCN и МСр являются подобными. Далее, площади подобных треугольников соотносятся как квадраты длин соответствующих сторон; но отношение соответствующих сторон NC и Ср такое же, как отношение площадей PNC и РСр (так как высоты этих последних треугольников одинаковы). Тогда отношение этих площадей - S:I; следовательно, отношение площадей PCN и MCp- S2: I2. Но площадь треугольника PCN определена как ½S; следовательно, площадь треугольника МСр равна
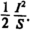
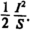
Таким же образом мы доказываем, что для малого изменения цены площадь треугольника ЕmР равна
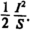
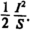
Поскольку S всегда положительна, эта величина также всегда положительна (как уже было показано).
Теперь мы можем записать формулы для величин всех наших вариаций. Если площадь внутреннего прямоугольника HPNh мы обозначим r, а площадь внешнего прямоугольника Hnph - R,8 обозначив четыре вариации следующим образом:
| компенсирующую по количеству | Сq |
| эквивалентную по цене | Cp |
| эквивалентную по цене | Ep |
| эквивалентную по количеству | Eq |
Эти формулы можно выразить следующим образом:
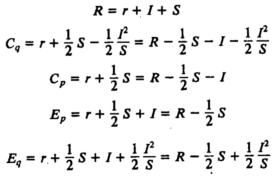
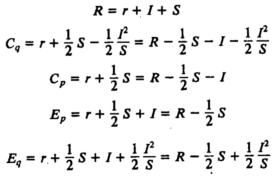
Мера Маршалла (приращение треугольника под кривой спроса):
r+½I+½S =R-½I - ½S.
Таким образом, она находится точно посередине между двумя вариациями по цене, посередине между двумя вариациями по количеству и (конечно) посередине между внутренним и внешним прямоугольниками.
Мы увидим, что
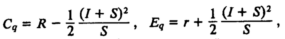
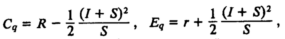
так что Cq всегда меньше R, а Eq всегда больше r, что действительно очевидно. (В точке М, например, потребитель имеет то же количество товара, что и в р, но он в худшем положении, чем в р; поэтому он, должно быть, заплатил за него больше).
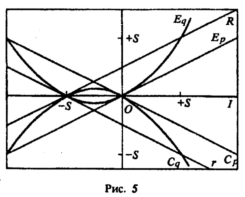 |
Отношения между нашими шестью величинами лучше всего показаны на графике, но на графике совсем другого вида. Примем S (эффект замены) за данное, и измерим все "вариации" и "прямоугольники" исходя из основания, находящегося посередине между всеми парами - иначе говоря, из меры Маршалла. Разница между каждой "вариацией" или "прямоугольником" исходя из меры Маршалла становится тогда функцией от I и ее можно вычертить как функцию от I. Это проделано на рис. 5.
Мы увидим, что если I / S малo и положительно, все четыре "излишка потребителя" лежат в промежутке между внутренним и внешним прямоугольниками; эквивалентные вариации больше, чем компенсирующие вариации; вариации по цене находятся между вариациями по количеству. Мы можем назвать это ортодоксальным случаем; это несомненно самый распространенный случай. Если I равно нулю, тогда, конечно, все "вариации" совпадают.
Существует, однако, целая плеяда "странных" возможностей. Одна из них будет иметь место даже при положительных эффектах дохода. Если I велико (I > S), четыре излишка потребителя все еще располагаются в своем ортодоксальном порядке, но вариации по количеству вышли за границы прямоугольников.
В случаях неполноценного блага может произойти все, что угодно. В наиболее распространенном случае, когда такая неполноценность мала, четыре излишка потребителя все еще находятся внутри прямоугольников, но вариации по цене теперь расположены снаружи вариаций по количеству, а компенсирующие и эквивалентные вариации поменялись местами. Первое, что происходит по мере усиления неполноценности - вариации по цене выходят за пределы прямоугольников. При I=-S кривая спроса поворачивается в обратном направлении, и таким образом два прямоугольника меняются местами. Поскольку внутренняя сторона прямоугольников стала внешней, вариации по количеству неминуемо выходят за их границы. И наконец, при I=-2S (но это уже совершенно экстремальный случай) вариации по количеству догоняют вариации по цене.
6. Это, по-видимому, завершает теорию приращения (или уменьшения) излишка потребителя, которая вытекает из малого изменения цены. Если рассматриваемое изменение цены велико, тогда невозможно уже более допускать, что линии PC и рЕ (рис. 3) будут параллельны, так что точная симметрия между компенсирующими и эквивалентными вариациями исчезнет. Далее, уже небезопасно допускать, что кривая спроса будет линейной, так что мера Маршалла перестает лежать точно посередине между двумя "прямоугольниками".
Тем не менее, даже когда изменение цены велико, должны выполняться три неравенства:
(1) Eq > Ep и Cq < Cp
(2) Eq > r и Cq < R
(3) Ep < R и Cp > r
Все это следует из рис. 3 и 4 безо всяких ограничений на размер изменения цены. Казалось бы, из этого следует, что, хотя другие отношения, показанные на рис. 5, не будут точны (график, так сказать, будет несколько более свободным и получит разброс), общий эффект будет в общем сходным.
Один из наиболее важных случаев большого изменения цены будет заключаться в том, что при более высокой цене товар вообще не будет приобретен; тогда мы будем иметь дело с "полным" излишком потребителя, который появляется в результате возможности приобрести товар по разумной цене, вместо того чтобы не иметь его вообще. Даже в этом случае все же надо различать наши четыре определения, хотя некоторые из них явно более важны, чем другие. В частности, если товар не просто недостижим для данного конкретного потребителя, а фактически вовсе не производится в одной из сравниваемых ситуаций, Еp перестает быть важной величиной, ибо Еp (измеряемая площадь HEph) зависит от конкретного уровня, на котором, как мы предполагаем, недоступная "цена" фиксирована, и которая, хотя мы знаем, что она больше ОА, в остальном абсолютно произвольна. С другой стороны, Еq (измеряемая треугольником hpm, поскольку m теперь находится на вертикальной оси) - величина, представляющая интерес. Это величина дополнительного дохода, который нужно было бы иметь потребителю, чтобы без товара ему было бы столь же хорошо, как при возможности получить его по цене Oh.
В основном рассмотрение именно этого случая заставило меня понять, что необходимо иметь теорию вариаций по количеству - теорию, которую я попытался представить в данной работе. Ибо, хотя в других случаях, возможно, более важны именно вариации по цене, нам обязательно нужно рассмотреть тот случай, когда товар исчезает вообще (это очень важный случай в Экономике Благосостояния9), и здесь нам нужно обратиться за помощью к вариациям по количеству.
В этой связи, видимо, особенно интересно одно из выдвинутых нами положений о вариации по количеству. Следует заметить, что во всех случаях, когда эффекты дохода положительны (рис. 3), кривая рЕm лежит выше кривой предельной оценки Арv, таким образом, когда m находится на вертикальной оси, она будет выше А. Далее, мы узнали, что в случаях, когда I велико относительно S, вполне возможно что рЕm будет пересекать вертикальную ось много выше A, настолько выше, что площадь треугольника mhp (m находится на вертикальной оси) будет, возможно, больше площади всего внешнего прямоугольника (который теперь стал внешним прямоугольником всей кривой спроса - прямоугольник с Ар в качестве диагонали). Такая возможность - это, конечно, экстремальный случай - проливает интересный свет на один из наиболее известных "парадоксов" излишка потребителей.
Предположим, мы имеем дело с абсолютно необходимым товаром - скажем, с продуктами питания вообще. За единицу "продуктов питания" мы можем взять минимум, необходимый для поддержания жизни на протяжении того периода, к которому относятся наши кривые. Если бы цена на продукты питания стала достаточно высокой, могло бы случиться - в экстремальном случае, - что весь доход был бы направлен на приобретение этой одной единицы продуктов питания. Это мы можем рассматривать как наиболее высокую точку, до которой может подняться кривая спроса, - это дает нам нашу точку А. Внешний прямоугольник кривой спроса может к тому времени стать очень большим, но все же это конечная величина. С другой стороны, эквивалентная вариация по количеству, не будет конечной величиной, поскольку не существует такой добавки к доходу, которая при отсутствии продуктов питания, достаточных для поддержания жизни, дала бы потребителю такое же благосостояние, какое он имеет при наличии достаточного количества продуктов питания. Это, конечно, экстремальный случай; но он должен укладываться в нашу теорию, и мы увидим, что так оно и есть. Эффект замены вдоль кривой рЕm, в конце концов становится равным нулю, поскольку по мере того, как мы поднимаемся по кривой вверх, она в конце концов становится параллельной вертикальной оси. Треугольник под кривой, следовательно, бесконечно велик.
7. Когда в одной из предыдущих работ я впервые взглянул на возможность такого анализа, который я провожу в данной статье, я отбросил его как "пустое дело, которое вряд ли будет иметь большое значение".10 И это все еще справедливо. Тем не менее, я рад, что заставил себя провести его. Поскольку потенциальные возможности методики Излишка Потребителя настолько велики (как в толковании, так и в дальнейшем развитии экономической теории), что стоит, видимо, сделать все, что может упрочить ее основы.Основы оказались сложными, но это ни в малейшей степени не делает концепцию излишка потребителей неприменимой. Во-первых, те различия, которые мы проводили, в большинстве случаев будут иметь малое зна-чение. Ни одна теория экономической политики не захочет обсуждать желательность мер, которые были бы связаны с пред-намеренным отказом от производства тех вещей, которые явля-ются абсолютно необходимыми, или даже тех вещей, которые в своей необходимости приближаются к абсолютной. Даже когда нас интересует полный излишек потребителя, так что мы действительно хотим рассмотреть полный отказ от некоторого товара (или введение нового товара), это почти всегда будет товар, который имеет хорошие заменители, так что эффект дохода должен быть малым относительно эффекта замены. Во всех таких случаях очевидно, что опасность ошибки при исполь-зовании методики Маршалла будет мала. Но это то, в чем нам нужно убедиться.
Во-вторых, даже если все-таки возникнет задача (что иногда будет происходить), в которой наши разграничения существенны, даже тогда они не доставят много беспокойства. Ибо сама задача определит, интересуемся ли мы вариациями по цене или вариациями по количеству. В случае налога, например, очевидно нужно рассматривать именно вариацию по цене; в случае нормирования потребления - вариацию по количеству. Противопоставление компенсирующих и эквивалентных вариаций может вызвать больше трудностей. Господин Скитовски в другой связи11 (но в действительности это тот же вопрос) отмечал, что мы с определенностью можем сказать только, что группа потребителей оказывается в лучшем положении в результате определенного изменения обстоятельств, если и компенсирующие и эквивалентные вариации (просуммированные для общего изменения обстоятельств и всех потребителей) показывают улучшение; потребители определенно оказываются в худшем положении, если обе вариации показывают ухудшение. Возможно (для группы, а не отдельного потребителя), что одна вариация указывает на выгоду, а другая - на ущерб, в этом случае будет невозможно рассматривать изменения как явное улучшение или явное ухудшение. Следовательно, если есть основание предполагать, что это две вариации могут ощутимо отличаться друг от друга, мы должны быть готовы сделать двойной расчет. Но поскольку на практике у нас вряд ли появится энтузиазм по поводу "улучшений", которые дают определенно положительную, но лишь малую выгоду, нас не слишком обеспокоит открытие того факта, что в экономическом положении возможны изменения, которые теоретически, а не только практически, нейтральны.
Наиболее важный результат нашего исследования носит, на мой взгляд, иной характер. Уже стало очевидным, что наиболее распространенная ошибка старой концепции излишка потребителей (не возьму на себя смелость обсуждать, насколько Маршалл был подвержен этой ошибке) заключается в том, что он рассматривался как абсолютная величина, когда утверждалось, что потребитель, просто потому, что он находится в таком-то и таком-то положении, получает такой-то и такой-то излишек. Новая концепция сильно отличается от этой. Излишек потребителей относителен, а не абсолютен. Мы всегда рассматриваем движение от одной определенной ситуации к другой определенной ситуации; мы спрашиваем, какое увеличение (или уменьшение) денежного дохода, которое могло бы измерить улучшение (или ухудшение) экономического благосостояния, являющееся результатом этого движения. Само это увеличение или уменьшение дохода должно всегда соотноситься с одной из двух ситуаций; в противном случае оно бессмысленно. Мы увидели, что даже в этом ограниченном значении излишек потребителей не является величиной точно выраженной; но теперь мы прояснили эти неопределенности (насколько сейчас видно) и, в конце концов, они не настолько непреодолимы. Излишек потребителей остается удобным инструментом анализа - столь же удобным, каким был всегда; и теперь нам надо научиться использовать его с большей уверенностью и большим доверием.
Надеюсь в еще одной статье применить настоящий метод, чтобы прояснить аналогичные неопределенности в концепции излишка производителей.
Манчестер
ПРИМЕЧАНИЯ:
i Review of Economic Studies. 1943. Vol. II. N 1. Р. 31-41.
1 J.R. Hicks.Value and Capital. P. 38-41; The Rehabilitation of Consumers' Surplus // Review of Economic Studies. February, 1941; Consumers'Surplus and Index Numbers Review of Economic Studies. Summer. 1942. В дальнейшем я буду ссылаться на них как на "Rehabilitation" u "Index-Numbers" соответственно.
2 Index-Numbers. P. 134.
3 См. ниже, примечание 7.
4 Index-Numbers; A. Henderson. Consumers' Surplus and Compensating Variation // Review of Economic Studies. February, 1941.
5 Index-Numbers. P. 128.
6 Henderson. Op. cit.
7 Таким образом, PC и PQ должны соприкасаться в Р; а рЕ и pq -в р. Прошу извинить за то, что это не очень хорошо видно на графике в том виде, как он нарисован. Это оправдание трактовки движения по кривой предельной оценки имеет те же свойства, что и кривая PC, которая является предельной кривой безразличия.
8 В "Index-Numbers" (поскольку там рассматривался более общий случай, это, видимо, было уместно) я называл их вариациями Ласпейреса (Laspeyres) и Паше (Paasche). Как будет видно далее, настоящий наш геометрический метод дает возможность получить формулы для вариации по цене более простым способом, и также добавить формулы для вариаций по количеству, которые можно, однако, подтвердить другим методом.





