Самые последние работы по проблеме (это я буду ниже доказывать) отличаются таким недостатком, как пренебрежение великими достижениями Фишера - нахождение оптимума через балансирование потребительских альтернатив во времени и ясное различение производственных и меновых возможностей. Вывод данного анализа (который нельзя здесь изложить подробно) заключается именно в том, что выдвинутые Боулдингом, Самуэльсоном, Скитовски и Лутцами предложения, касающиеся решения проблемы определения оптимального объема инвестиций, по меньшей мере частично неправильны. Ошибку, присущую им всем, следует искать в правиле или формуле, иллюстрирующей оптимальные инвестиционные решения независимо от потребительских решений. Такой поиск не может быть успешным при правильности фишеровского анализа, согласно которому инвестиции - сами по себе не цель, а скорее процесс распределения потребления во времени.
В данной статье рассматривается очень упрощенная ситуация, в которой затраты и доходы, связанные с альтернативными инвестициями отдельного индивида, известны с определенностью. В такой ситуации существует проблема выбора объема и структуры инвестиций, которые нужно осуществить. Мы начнем анализ на основе предпосылки об ограниченности инвестиционных решений лишь двумя периодами времени. В последующих разделах будет видно, что двухпериодный анализ можно сразу трансформировать в анализ инвестиций в пожизненную ренту. Однако в более общем случае колебаний потоков доходов возникают дополнительные трудности, решение которых поднимает новые принципиальные вопросы. Конечно, ограничение анализа допущением совершенной информации является неблагоприятным, поскольку неведение и неопределенность представляют собой сущность любого реального инвестиционного решения. Тем не менее анализ оптимальных решений в условиях определенности можно оправдать в качестве первого этапа на пути выработки более совершенной теории. В качестве защиты этого сверхупрощенного допущения мы лишь предложим тезис о том, что экономисты-теоретики сильно расходятся в мнениях по поводу того, будет ли представлять собой реальный вклад в науку успешная попытка нахождения оптимального решения в рамках стандартной экономической теории.
I. Двухпериодный анализ
1. Ставка заимствования равна ставке кредитования (решение Фишера)
Для того чтобы заложить основы для последующего анализа трудных проблем, мы дадим сначала обзор фишеровского решения проблемы нахождения оптимальных инвестиций.3 Рассмотрим случай, характеризующийся следующими условиями. Имеется ставка процента, по которой индивид (или фирма)4 может брать деньги взаймы; при этом она не зависит от величины взятых им займов. Существует также процентная ставка, по которой он может давать деньги в долг; она также не зависит от объема предоставленных им кредитов. Обе эти ставки равны друг другу. Данные условия использовались Фишером; их наличие означает, что рынок капитала является совершенным.
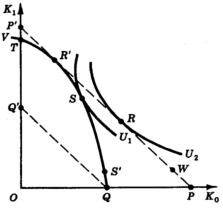 Рис.1. Решение Фишера. |
На рис. 1 горизонтальная ось, K0, отображает величину фактического или потенциального дохода (потребляемого или доступного для потребления) в период 0; вертикальная ось, K1 представляет величину дохода (имеющего тот же экономический смысл) в период 1. Проблема индивида заключается в выборе - с учетом доступных для него возможностей - оптимальной точки на графике, т. е. оптимальной временной структуры потребления. Его начальная точка может быть точкой на любой из осей (тогда первоначальный доход достается ему либо полностью в период 0, либо полностью в период 1), например точкой Т или Р, или же точкой в положительном квадранте (первоначальный доход достается индивиду частично в период 0 и частично в период 1), например точкой W или S'. Она может находиться даже во втором или четвертом квадранте; тогда исходная ситуация характеризуется отрицательным доходом либо в период 0, либо в период 1.
Предполагается, что индивид имеет функцию предпочтения относительно своего дохода в периоды 0 и 1. Функция предпочтения отображается обычным способом, и кривые U1 и U2 представляют собой обыкновенные кривые безразличия.
Наконец, для индивида открыты инвестиционные возможности. Фишер проводит различие между "инвестиционными возможностями" и "рыночными возможностями". Первое - реальные производственные трансферты между доходом в один период времени и доходом в следующий период (это то, что мы обычно называем физическими инвестициями, например посев семян); второе - трансферты, связанные с заимствованием или кредитованием (объемы которых, естественно, в целом уравновешиваются на рынке ссуд). Я должен здесь отказаться от использования фишеровских терминов, для того чтобы провести более четкое различие между "производственными возможностями" и "рыночными возможностями"; слово "инвестиции" будет употребляться в более широком смысле и относиться к возможностям обоих типов, рассматриваемым вместе. Таким образом, мы можем осуществить инвестиции, построив дом (жертвуя сегодняшним доходом ради будущего дохода за счет производственных возможностей) или ссудив средства на денежный рынок (жертвуя сегодняшним доходом ради будущего дохода за счет рыночных, или меновых, возможностей). Для описания рыночных возможностей мы можем также говорить не о кредитовании или заимствовании, а о покупке и продаже капитальных активов.
На рис. 1 инвестор, находящийся в начальной точке Q, имеет рыночные возможности, иллюстрируемые прерывистой линией QQ'. Иными словами, ему доступен весь его доход в период 0; при этом он может предоставить его в ссуду при некоторой данной ставке кредитования, жертвуя сегодняшним доходом ради будущего; он может, таким образом, отдать любую сумму, не превышающую K0, получив в обмен K1 или доход в период 1. Мы также можем сказать, что он может купить капитальные активы - титулы собственности на будущий доход K1, имея текущий доход K0. Вслед за Фишером я называю QQ' рыночной линией.5 Линия PP', параллельная QQ', представляет собой рыночную линию, доступную для индивида, чья начальная точка - точка Р на оси K0. При принятии допущения о том, что ставка заимствования также постоянна и равна ставке кредитования, рыночная линия PP' представляет собой также рыночную возможность для индивида, начальная точка которого - точка W в положительном квадранте.
Наконец, кривая QSTV показывает диапазон производственных возможностей, доступных для индивида в начальной точке Q. Этот диапазон представляет собой геометрическое место точек, достижимых индивидом, по мере того как он жертвует все большей и большей суммой K0, осуществляя производственные инвестиции, приносящие ему доход K1. Это геометрическое место точек Фишер несколько двусмысленно называл "линией возможностей"; здесь оно будет называться кривой производственных возможностей, или кривой производственной трансформации. Следует отметить, что, поскольку кривая вогнута относительно начала координат, имеет место убывающая доходность инвестиций. Более конкретно производственные инвестиционные проекты можно ранжировать на основе выражения ΔK1/(-ΔK0)-1, которое может быть названо производственной нормой дохода.6 Здесь ΔK0 и ΔK1 представляют собой (связанные с реализацией данного проекта) изменения дохода соответственно в периоды 0 и 1.
Мы можем ранжировать приведенным способом все проекты; в этом случае мы получим среднюю производственную норму дохода по каждому такому проекту. Или же мы можем ранжировать бесконечно малые приращения к стоимости проектов; тогда мы можем вывести предельную производственную норму дохода. Кривая QSTV будет непрерывной и иметь непрерывную первую производную при определенных условиях, касающихся "цельности" (lumpiness) отдельных проектов (или приращений их стоимости), в которые нам не нужно вдаваться. В любом случае QSTV будет представлять собой последовательность проектов, начинающуюся с проекта, приносящего наивысшую производственную норму дохода справа внизу, и заканчивающуюся проектом с самой низкой нормой дохода, получамого, когда жертвуется последний доллар из дохода периода 0, слева вверху.7 Та часть QSTV, которая расположена во втором квадранте, также может иметь экономический смысл, когда K0 становится отрицательным. Конечно, точки, расположенные в этой части, не будут оптимальными при наличии кривых безразличия, изображенных на рис. 1, но тем не менее могут "принять участие" в определении оптимума. (В этом анализе допускается, что проекты независимы. При снятии этого допущения возникает более сложная ситуация, рассматривающаяся ниже, в разделах 5 и 6).
Перейдем теперь непосредственно к нахождению оптимума. Цель инвестора - достичь как можно более высокой кривой безразличия. Двигаясь вдоль линии производственных возможностей QSTV, он видит, что наивысшая кривая безразличия касается U1 в точке S. Но это не лучшая точка из потенциально достижимых, поскольку он может двигаться вдоль QSTV несколько далее, до точки R', которая расположена на рыночной линии PP'. После этого он может смещаться в обратном направлении (беря деньги взаймы), и тогда наилучшей достижимой точкой становится точка R на кривой безразличия U2.
Таким образом, решение инвестора реализуется в два этапа. "Производственным" решением - точкой, в которой индивид прекращает осуществление дополнительных производственных инвестиций, - является точка R'. Затем он может двигаться вдоль рыночной линии до точки, более полно удовлетворяющей его временные предпочтения; этой точкой является точка R. Иными словами, индивид осуществляет наилучшие инвестиции с производственной точки зрения и затем "финансирует" их, пользуясь кредитным рынком. Весьма типичным примером из реальной жизни могут здесь послужить строительство дома и последующее взятие денег в долг под закладную по мере поступления текущего потребительского дохода.
В свете этого решения мы можем теперь рассмотреть сегодняшнюю дискуссию между сторонниками двух конкурирующих правил оптимального инвестиционного поведения.8 Согласно первому из них - правилу сегодняшней ценности, индивид или фирма согласны на реализацию всех проектов, чья сегодняшняя ценность больше нуля при данной рыночной процентной ставке. Фирма максимизирует сегодняшнюю ценность доходов обоих периодов (0 и 1). При имеющихся на данный момент условиях сегодняшнюю ценность можно определить как K0+K1/(1+i). Здесь доход периода 1 дисконтируется множителем 1+i, где i - ставка заимствования-кредитования. Так как рыночные линии определяются условием, в соответствии с которым жертва 1 дол. из дохода K0 приносит (1+i) дол. дохода K1, эти линии не что иное, как линии постоянной сегодняшней ценности. Уравнения этих линий таковы: K0+K1/(1+i)=C, где С - параметр. Согласно правилу сегодняшней ценности, инвестирование, позволяющее достичь самой высокой из таких линий, возможно и имеет место в точке R'. До сих пор правило сегодняшней ценности работает хорошо, но с его помощью ничего нельзя выяснить по поводу финансирования (заимствования или кредитования), которое также необходимо для того, чтобы достичь конечного оптимума - точки R.
Правило внутренней нормы дохода в рассматриваемом здесь виде заключается в том, что фирма согласна на реализацию любого проекта, чья внутренняя норма дохода выше рыночной процентной ставки. В общем случае внутренняя норма проекта определяется как норма дисконтирования r, в соответствии с которой происходит уменьшение потока чистых доходов, порождаемых проектом, до сегодняшней ценности, равной нулю (иными словами, эта норма приравнивает дисконтированную ценность потоков затрат на проект к дисконтированной ценности потока поступлений). Мы можем записать:
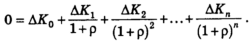
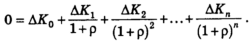
В двухпериодном случае ρ идентично производственной норме дохода: ΔK1/(-ΔK0)-1. Как и в приведенном выше анализе, если допускаются бесконечно малые изменения, мы можем этот тезис интерпретировать в предельном смысле. Предельная (двухпериодная) внутренняя норма дохода измеряется наклоном кривой производственных возможностей за вычетом единицы. На рис. 1 на каждом этапе мы сопоставляем наклон линии QSTV с наклоном рыночных линий. Мы будем двигаться вдоль линии QSTV до тех пор и только до тех пор, пока она круче, чем рыночные линии. Очевидно, что в соответствии с этим правилом движение по линии QSTV закончится там, где она станет касательной к рыночной линии в точке R'. Опять-таки до сих пор правило внутренней нормы дохода дает хорошие результаты, но с его помощью нельзя что-либо сказать о заимствовании или кредитовании, которые, как уже подчеркивалось, также необходимы для достижения оптимума.
Можно сделать вывод, что по меньшей мере в двухпериодной ситуации правило сегодняшней ценности и правило внутренней нормы дохода приводят к идентичным итогам,9 которые аналогичны результатам, получаемым за счет применения нашего анализа изоквант, но только в том случае, если он не распространяется за рамки изучения производственных инвестиционных решений. Оба правила не дают никакой информации о рыночных обменах K0 на K1, которые остаются обязательными для достижения оптимума. Этот второй этап - очевидно, часть решения. Если бы возможность брать и давать в долг отсутствовала, то точка S была бы наилучшей из достижимых и процесс производственных инвестиций не нужно было бы осуществлять для достижения точки R'. Однако мы не можем с определенностью сказать, что эти правила ошибочны, поскольку нет таких рыночных возможностей, которые не содержали бы рыночную процентную ставку i, используемую для вычисления сегодняшней ценности или для сопоставления с предельной внутренней нормой дохода. Нам остается рассмотреть, можно ли эти правила переформулировать или обобщить, чтобы применить их к ситуациям, в которых невозможно неограниченное заимствование и кредитование по рыночной процентной ставке. Но можно заметить, что в сравнении с анализом изоквант каждое из этих правил дает только частичный результат.
2. Ставки заимствования и кредитования различны
Мы можем теперь отклониться от фишеровского анализа или, скорее, расширить его применительно к ситуации, которую он не рассматривал. Мы по-прежнему допускаем постоянство ставок кредитования и заимствования независимо от сумм, которые дает или берет в долг рассматриваемый индивид (или фирма). Однако теперь мы принимаем предпосылку, согласно которой эти ставки не равны друг другу и ставка заимствования выше ставки кредитования.10 На рис. 2 изображена та же самая карта безразличия, что и на предыдущем рисунке; на ней показана лишь изокванта U1. Однако теперь на графике проведены две разные рыночные линии; более крутая (прерывистая) линия описывает возможности заимствования (обратите внимание на направления стрелок), а более пологая (сплошная) линия отображает возможности кредитования. S'S и W'W показывают два возможных диапазона производственных возможностей, каждый из которых позволяет сделать выбор вдоль U1. Начиная свою деятельность с величины OW дохода K0, инвестор с производственными возможностями WVW' будет двигаться вдоль WVW' до V, а затем вдоль линии возможностей кредитования. Объем предоставленных им кредитов, позволяющий достичь оптимума временных предпочтений, будет найден им в точке касания V' этой линии с U1. Кривая STS' описывает гораздо большие производственные возможности; первоначально имея только OS дохода K0, инвестор будет двигаться вдоль STS' до T, а затем брать займы, возвращаясь назад по прерывистой линии до точки T', в которой данная линия касается U1. Следует отметить, что общий диапазон возможностей (точки, достижимые за счет любой комбинации рыночных и производственных возможностей) описывается следующими линиями: WVV* для первой возможности и S'TT* для второй.
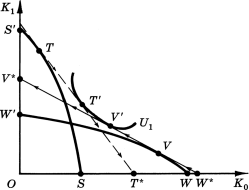 Рис.2. Расширение анализа Фишера для неравных ставок заимствования и кредитования. |
Однако более детальный анализ показывает, что мы еще не имеем полного решения, ведь существует еще третья возможность. Инвестор с производственными возможностями, начинающий деятельность на оси K0, никогда не перестанет двигаться вдоль геометрического места точек этих возможностей в направлении большего K1, до тех пор пока предельная производственная норма дохода превышает ставку заимствования, и не захочет смещаться на те участки данной линии, где предельная производственная норма дохода оказывается ниже ставки кредитования. Предположение, согласно которому можно осуществить некоторые исходные инвестиции, приносящие производственную норму дохода, превышающую ставку заимствования, означает, что инвестор будет двигаться вдоль линии производственных возможностей, до тех пор пока не окажется достигнутой ставка заимствования, равная производственной норме дохода. Если в этой точке можно двинуться к более высокой кривой безразличия посредством займов, то производственные инвестиции должны прекратиться и индивид будет брать деньги в долг, попадая в точку типа точки T на рис. 2. Однако если заимствование сокращает полезность, то произойдет увеличение производственных инвестиций. Теперь допустим, что инвестиции осуществляются до тех пор, пока в соответствии с принципом убывающей доходности предельная производственная норма дохода не снизится до ставки кредитования. Тогда если кредитование повышает полезность, то производственные инвестиции прекратятся и будет иметь место ссужение. Инвестор попадет в точку, подобную точке V на рис. 2. Но предположим, что сейчас выяснилась следующая зависимость: кредитование также уменьшает полезность! Это может только означать, что касание геометрического места точек производственных возможностей и кривой безразличия произошло тогда, когда предельная производственная норма дохода оказалась где-то между ставкой кредитования и ставкой заимствования. В такой ситуации не нужны ни заимствование денег в долг, ни предоставление их в кредит; оптимум достигается прямо за счет производственных инвестиций, увеличиваемых настолько, чтобы приравнять предельную производственную норму дохода предельной норме замещения (в смысле временных предпочтений) вдоль изокванты полезности.
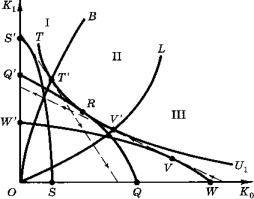 Рис.3. Три зоны оптимумов при разнице в ставках заимствования и кредитования. |
Описанные только что решения иллюстрируются разделением рис. 3 на три зоны. В зоне I ведущую роль играет ставка заимствования. Оптимум, при котором имело место касание с рыночной линией в точке типа точки Т на рис. 2, на данном рисунке смещен ниже за счет заимствования до такой точки касания с изоквантой полезности, как точка T'. Все подобные точки конечного оптимума расположены вдоль кривой OB; эта кривая соединяет все точки на изоквантах полезности, в которых наклон этих изоквант равен наклону рыночной линии заимствования. Аналогичным образом зона III - это область, в которой оптимальное производственное решение связано с касанием рыночной линии кредитования (в точке V); по сравнению с рис. 2 этот оптимум смещается выше за счет кредитования до такой точки касания с изоквантой полезности, как V'. Эта точка конечного оптимума лежит на кривой OL - данная линия соединяет все точки на изоквантах полезности, в которых наклон этих изоквант равен наклону рыночной линии кредитования. Наконец, в зоне II оптимум достигается, когда геометрическое место точек производственных возможностей типа QRQ' имеет более крутой наклон, чем линия кредитования на протяжении всей зоны III, но в то же время более пологий, чем линия заимствования на протяжении всей зоны I. Поэтому такое геометрическое место точек должно касаться одной из кривых безразличия где-то в зоне II.
По аналогии с анализом, приведенным в предыдущем разделе, мы можем сделать вывод о том, что ставка заимствования будет приводить к правильным решениям (касающимся выбора производственных инвестиций при пренебрежении вопросом финансирования) при использовании правила сегодняшней ценности или правила внутренней нормы дохода тогда, когда оптимум расположен в зоне I. Аналогичным образом ставка кредитования будет приводить к правильным инвестиционным решениям, если оптимум находится в зоне III. Однако если оптимум расположен в зоне II, ни одна из этих ставок не годится для его конкретного определения. В таком случае правильные результаты даст некая ставка, которая (по величине) находится между ставками кредитования и заимствования. Иными словами, мы могли бы охарактеризовать эту правильную ставку дисконта как предельную норму производственных возможностей,11 которая в равновесии будет равна предельной норме субъективных временных предпочтений. В данной ситуации ни одно из правил не подходит для нахождения производственного оптимума без использования изоквант полезности; однако все, что здесь необходимо знать, - это информация о наклонах изоквант и границах производственных возможностей. Конечно, даже когда рассматриваемые правила удовлетворительны, они все равно вводят в заблуждение, наводя на мысль о том, что можно принять правильные производственные инвестиционные решения независимо от финансового решения.
Возможно, в ретроспективе это решение кажется очевидным. В ситуации, в которой производственные возможности, временные предпочтения и рыночные (или финансовые) возможности находятся в таких отношениях друг к другу, что возникает необходимость заимствования для достижения оптимума, ставка заимствования - правильная ставка в смысле ее использования для определения оптимального производственного инвестиционного решения. Ставка кредитования в этом случае не годится для подобного использования, так как оптимальное решение содержит балансирование затрат, связанных с заимствованием, и дохода от дальнейших производственных инвестиций, а обе величины превышают эту ставку. Возможности кредитования на самом деле пока еще доступны, но, поскольку норма дохода от кредитования меньше самой низкой предельной производственной нормы дохода, мы хотели бы принимать решение, учитывая ставку заимствования, по которой нам придется возвращать долги; и в такой ситуации кредитование - неуместная альтернатива. Адекватной альтернативой производственным инвестициям здесь скорее является сокращение объемов заимствования, которое принесет большее вознаграждение в смысле экономии на процентах, чем кредитование. Аналогичным образом, когда соображения балансирования диктуют необходимость предоставления в кредит части текущих фондов фирмы, заимствование не годится для финансирования производственных инвестиций. Разумной альтернативой увеличению производственных инвестиций является отсрочка кредитования. Хотя подобные рассуждения, возможно, очевидны, в экономической литературе можно найти разногласия по вопросу о том, является ли ставка кредитования или заимствования единственной правильной ставкой.12
3. Возрастающие предельные затраты заимствования
Хотя допущение постоянства ставки кредитования (согласно которому действия инвестора по предоставлению кредитов не приводят к снижению этой ставки) в целом, пожалуй, следует рассматривать как удовлетворительное, из-за практических соображений важно принять во внимание случай, в котором увеличение объемов заимствования может иметь место только при возрастании связанных с ним затрат. Однако, когда такое усложнение имеет место, оно не требует какой-либо существенной модификации нашей модели.
Как и предыдущие рисунки, рис. 4 иллюстрирует геометрическое место точек производственных возможностей и кривую безразличия U1. В целях упрощения предположим, что предельные затраты, связанные с заимствованием, растут с одинаковым темпом независимо от того, начинает ли инвестор брать в долг в точке R', S', W' или в какой-либо другой точке вдоль линии QR'T (конечно, он не может начать занимать в точке Q, вообще не имея K1, необходимого для обмена на большее количество K0). При этом допущении мы можем построить рыночные кривые, вогнутые к началу координат, например R'R, S'S и W'W. Кривая TE описывает общий диапазон возможностей, будучи огибающей эти рыночные кривые; иными словами, TE соединяет все точки на рыночных кривых, представляющих собой максимальную величину K0, достижимую для любого данного K1. В соответствии с сущностью огибающей кривой TE будет касаться рыночной кривой в каждой такой точке. Найти оптимум теперь просто - это точка касания TE наивысшей из достижимых кривых безразличия; в данном случае такой точкой является точка R. Чтобы достичь R, инвестор должен использовать свои производственные возможности вплоть до точки R', а затем "сместиться назад" вдоль своей рыночной кривой заимствования до R.
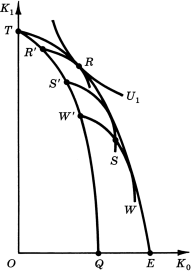 Рис.4. Возрастающие предельные затраты заимствования. |
Только что проведенный анализ применим лишь к оптимуму, наблюдающемуся в зоне I (заимствования) согласно классификации предыдущего раздела. В зависимости от природы производственных возможностей при допущениях, принятых в настоящем разделе, оптимум также может находиться в зоне II или III. Однако выводы, касающиеся роли правил сегодняшней ценности и внутренней нормы дохода, являются неизменными по отношению к этим двум зонам. Только для оптимума зоны I имеется некоторая модификация.
Как всегда, важнейшим вопросом, касающимся этих правил, является вопрос о том, какая ставка дисконта используется. Интуиция подсказывает нам, что в качестве такой ставки для определения оптимума в зоне I должна употребляться ставка, представляющая собой предельные затраты, связанные с заимствованием, поскольку производственные инвестиции будут осуществляться только до той точки, которая оправдана затратами, связанными с соответствующим увеличением объемов заимствования.13 Иными словами, наклон изгиба в любой точке, лежащей на огибающей кривой (например, в точке R), равен наклону кривой производственных возможностей в соответствующей точке (R'), т. е. соединенной с предыдущей точкой (R) рыночной кривой.14 Если оптимум действительно находится в зоне I, то ставка дисконта, определенная наклоном при касании с U1 в точке типа R, будет также приводить к увеличению производственных инвестиций вплоть до точки R' согласно рассмотренным правилам. Конечно, это утверждение опять-таки чисто формально. Строго говоря, эти правила могут не иметь большой ценности, поскольку ставка дисконта, которая будет использоваться, заранее неизвестна независимо от функции полезности (временных предпочтений).
4. Рационирование капитала - текущие дебаты
Предыдущий анализ содержит ключ к решению проблемы, вызывающей сегодня оживленные дискуссии; эта проблема касается факторов, определяющих оптимальные инвестиции при условиях рационирования капитала или фиксированного бюджета капиталовложений. Отмечают, что это ограничение имеет место, когда фирма (или индивид, или даже какой-либо административный орган правительства) не может взять в долг дополнительное количество капитала и поэтому ей (ему) остается заниматься наилучшим использованием капитала, которым она (он) уже фактически обладает или который вот-вот поступит в ее (его) распоряжение.15 В теоретической экономической литературе очень близкую идею высказывал Скитовски, который, рассматривая доступность капитала в смысле текущих капитальных фондов как фиксированный фактор, ограничивающий размер фирмы, выдвигал в качестве инвестиционного критерия максимизацию "прибыли на единицу вложенного капитала".16 Лутцы, напротив, в качестве инвестиционного критерия принимали максимизацию нормы дохода на собственный предпринимательский капитал, трактовавшийся ими как фиксированный.17
Интересно проанализировать эти идеи более детально, используя аналитический инструментарий рассматриваемой нами фишерианской модели. Скитовски определял капитал как текущие капитальные фонды (наше K0), требуемые для того, чтобы заполнить временной разрыв между затратами на закупку факторов производства и получением выручки за реализацию выпуска.18 Однако при принятии этого определения капитал будет фиксирован для фирмы лишь тогда, когда имеют место особые условия, а именно если существует разрыв (отсутствие непрерывности) на рынке капитальных фондов, состоящий в том, что предельная ставка заимствования внезапно становится бесконечно большой при определенном объеме займов со стороны фирмы.19 При отсутствии такого разрыва бесконечно большая предельная ставка заимствования никогда не будет представлять равновесное состояние для заемщика, если его предпочтение сегодняшнего дохода по сравнению с будущим не является абсолютным. И конечно, если предельная ставка заимствования небесконечна, нельзя сказать, что текущие капитальные фонды фиксированы. Тем не менее, хотя этот случай может считаться особым и вряд ли возможным в реальности, он приемлем в качестве разумного приближения к определенным ситуациям, складывающимся на практике, особенно, вероятно, в коротком периоде при ошибках в предыдущих расчетах. Можно сказать, что, когда подразделение фирмы или административный орган правительства сталкиваются с бесконечной предельной ставкой заимствования, бюджетное ограничение полностью достигнуто - до тех пор, пока после следующего заседания совета директоров или Конгресса не будут предоставлены дополнительные фонды.
С другой стороны, трудно понять, что имеют в виду Лутцы, когда говорят о фиксированности собственного капитала фирмы. В фишерианском анализе собственность на сегодняшние или будущие активы является юридической формулировкой, не имеющей аналитического значения. Покупка актива, приносящего будущий доход за счет текущих фондов, не что иное, как просто кредитование; тогда как продажа дохода - то же самое, что и заимствование. Однако в более глубоком смысле мы можем думать о фирме как о собственнике доступного для нее диапазона возможностей или по меньшей мере физических производственных альтернатив; возможно, это то, что имели в виду Лутцы. Таким образом, дом Робинзона Крузо может рассматриваться в качестве его "собственного капитала" - ресурса, приносящего потребительский доход как в настоящем, так и в будущем. Трудность состоит в том, что, по-видимому, Лутцы употребляют термин "собственный капитал" для описания ценности производственных ресурсов (в виде капитальных благ), которыми владеет фирма;20 но собственные физические капитальные блага нельзя конвертировать в ценность капитала, не введя в анализ нормы дисконтирования потоков поступлений. Однако, как мы видели выше, поскольку ставка дисконта, необходимая для принятия оптимальных решений фирмой, не является независимой величиной (за исключением случая существования совершенного рынка капитала), но сама определяется моделью, ценность капитала в общем и целом нельзя рассматривать как фиксированную величину независимо от инвестиционных решений.21
Хотя рамки статьи не позволяют привести полную критику важной работы Лутцев, следует упомянуть, что в соответствии с фишерианской точкой зрения эта работа базируется на неверных исходных предпосылках. Лутцы сперва искали окончательный критерий или формулу в качестве правила для определения оптимальных инвестиций и чисто интуитивно выбрали таким критерием максимизацию нормы дохода на собственный капитал инвестора. Напротив, фишерианский подход интегрирует инвестиционные решения в общую теорию выбора; здесь целью является максимизация полезности при наличии определенных возможностей и ограничений. В этом контексте можно обосновать конкретные формулы в качестве полезных (взятых в первом приближении) правил для решения проблем определенных типов - это я попытаюсь здесь продемонстрировать. Однако окончательный фишерианский критерий выбора - оптимальное балансирование потребительских альтернатив во времени - не может быть сведен к какой-либо из обычных формул.
Вместо того чтобы углубляться в дальнейшее изучение различных значений, которые может иметь фиксированность капитала фирмы, более полезным будет рассмотрение того, как фишерианский подход позволяет решить проблему рационирования капитала. Я должен здесь использовать в качестве иллюстрации случай (его можно назвать "ситуацией Скитовски"), когда инвестор сталкивается с разрывом (отсутствием непрерывности) на рынке, что делает предельную ставку заимствования бесконечно большой. Я рассматриваю данный случай (являющийся, по моему мнению, эмпирически значимым только в коротком периоде) в качестве основы для анализа рационирования капитала.
Бесконечная ставка заимствования означает, что рыночные линии заимствования, показанные прерывистыми линиями на рис. 2 и 3, вертикальны. В результате кривая OB на рис. 3 сдвигается влево настолько далеко, что зона I полностью теряет свое значение как места, в котором может находиться оптимум. Последний может быть теперь лишь в зонах II и III. Геометрическое место точек инвестиционных возможностей типа WVW' на рис. 3 становится менее крутым, чем рыночная кривая кредитования в зоне III. В данной ситуации инвестор будет увеличивать капиталовложения до точки V, где эти наклоны снова равны друг другу, и затем предоставлять в кредит деньги, до тех пор пока не будет достигнута точка касания V', которая лежит где-то на кривой OL на рис. 3. Если же геометрическое место точек инвестиционных возможностей типа QRQ' на рис. 3 еще круче, чем рыночная кривая кредитования после того, как первая из них пересекает OL, то инвестиции должны осуществляться до касания с кривой безразличия типа U1; это касание достижимо где-то слева от линии OL при отсутствии кредитования или заимствования.
При использовании правил сегодняшней ценности, или внутренней нормы дохода, в вышеописанной ситуации решения должны основываться на ставке кредитования (используемой в качестве нормы дисконтирования или стандарта сопоставления), в том случае если оптимум находится в зоне III. Здесь уже имеет место кредитование, так как движение вверх и влево остается еще желательным, когда самые последние из сделанных инвестиций приносят больший доход, чем ставка по кредитам. Если же оптимум находится в зоне II, то ставку кредитования не следует употреблять. Инвестиции, характеризующиеся положительной сегодняшней ценностью при данной ставке кредитования (или, иными словами, отличающиеся внутренней нормой дохода, превышающей эту ставку), будут тем не менее нежелательными, после того как окажется достигнутой точка касания, в которой становятся равными друг другу наклоны кривой инвестиционных возможностей и кривой временных предпочтений. Короче говоря, правильной нормой здесь является предельная ставка (норма) возможностей.
Оптимум изменится лишь незначительно, если мы рассмотрим изолированного индивида типа Робинзона Крузо или замкнутое сообщество вроде страны, функционирующей в условиях автаркии (или же мировой экономики в целом). В такой ситуации невозможны ни заимствование, ни кредитование (в нашем смысле этих слов); существуют лишь производственные возможности. Это означает, что оптимум может находиться только в зоне II. Описанный случай - пример наиболее экстремального отхода от предпосылки совершенных рынков капитала.22
Как и в случае с оптимумом, находившимся в зоне II при отсутствии рационирования капитала, правила сегодняшней ценности и внутренней нормы дохода можно формально модифицировать в целях применения к ситуации, при которой оптимум пребывает в той же зоне, но уже при наличии упомянутого рационирования. Ставка дисконта, используемая для вычисления сегодняшней ценности или в качестве стандарта сопоставления с внутренней нормой дохода от прироста стоимости проекта, определяется наклоном кривой инвестиционных возможностей в точке ее касания кривой полезности в зоне II (иными словами, эта норма представляет собой предельную производственную норму дохода); при использовании этой нормы вышеназванные правила позволяют правильно определить оптимум. Но эту норму невозможно определить, пока не найдено оптимальное решение, и поэтому ее применение не сможет помочь в обеспечении такого решения. Исключением является случай с нахождением оптимума в зоне III; этот случай содержит кредитование, возникающее в ситуации Скитовски. Здесь, конечно, должна употребляться ставка кредитования. В то же время не используется неопределенная ставка дисконта, дающая верные результаты, когда правила, применяемые при выявлении оптимумов, пребывающих в зоне II, могут рассматриваться в качестве разновидности теневой цены, отражающей производственную норму дохода, обеспечиваемого наилучшей альтернативной возможностью.
Читателя может заинтересовать следующий аспект. Почему в ситуации Скитовски результатом анализа оказался не результат Скитовски? Последний заключался в том, что оптимальное инвестиционное решение максимизирует (среднюю) внутреннюю норму дохода на сегодняшние капитальные фонды фирмы (K0). Таким образом, на рис. 3 для фирмы, начинающей свою деятельность с OQ дохода K0 и имеющей производственные возможности, описываемые геометрическим местом точек QRQ', средняя норма дохода (K1, полученного на единицу пожертвованного K0) представляет собой максимум при бесконечно малом движении вдоль QRQ', поскольку чем дальше происходит сдвиг, тем больше снижаются предельная и средняя производственные нормы дохода. Такое правило приводит к выводу об оптимальности неизменного пребывания в точке Q, что является, очевидно, ошибочным решением.
Как же данное обстоятельство можно согласовать с интуитивно правдоподобным аргументом Скитовски, согласно которому фирма всегда пытается максимизировать свой доход от фиксированного фактора и при этом нужно допускать неизменность сегодняшних капитальных фондов?23 Ответ на этот вопрос состоит в следующем. Приведенный аргумент применим только к фактору, который фиксирован в смысле отсутствия альтернативных сфер его использования. В нашем анализе допускалась фиксированность сегодняшних капитальных фондов K0, но не в том смысле, который имел в виду Скитовски. Употребление этого понятия нами означает, что нельзя осуществить дополнительное заимствование, но в то же время признается возможность потребления сегодняшних фондов в качестве альтернативы их вложению. Однако в теории Скитовски фонды должны инвестироваться. Если бы в действительности текущий доход K0 нельзя было бы использовать иначе, кроме обмена на будущий доход K1 (такая предпосылка означает абсолютное предпочтение будущего дохода по сравнению с текущим доходом), то ситуация Скитовски позволяет определить, как достичь наивысшей точки на оси K1.24 На самом деле наши временные предпочтения в большей степени сбалансированы; альтернативный способ использования K0 (потребление) реально существует. Поэтому даже в ситуациях Скитовски мы будем выбирать такие значения K0 и K1, которые приносят нам наибольшую полезность, а не просто принимать максимум K1, который мы можем получить в обмен на все наше фиксированное K0.25 Исследования, проведенные Скитовски, Лутцами и многими другими экономистами в последнее время, часто приводят к ошибочным результатам из-за отсутствия учета альтернативных возможностей потребления, которые Фишер интегрировал в свою теорию инвестиционных решений.
5. Взаимоисключающие инвестиционные возможности
Вплоть до настоящего момента мы вслед за Фишером допускали независимость инвестиционных возможностей, в результате чего их можно было ранжировать каким-либо желаемым образом. В частности, они были классифицированы на рис. 1-4 на основе принципа убывающей производственной нормы дохода; имевшая место вследствие применения этого принципа вогнутость порождала единственное оптимальное решение в точке касания кривой инвестиционных возможностей с кривой полезности или с рыночной кривой. Но предположим теперь, что существуют два взаимоисключающих (mutually exclusive) набора таких инвестиционных возможностей. Приняв подобное допущение, мы можем рассмотреть строительство фабрики на Востоке или на Западе, но не то и другое вместе. Пусть возможности вложений на Востоке выглядят как геометрическое место точек QV'V, а возможности вложений на Западе - как QT'T на рис. 5.26
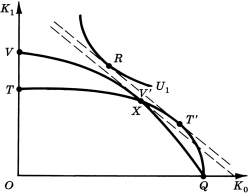 Рис.5. Взаимоисключающие инвестиционные возможности - два геометрических места точек альтернативных производственных инвестиций. |
Какая из этих возможностей лучше? Фактически нахождение оптимального решения по-прежнему следует из принципов Фишера, хотя слишком большая степень взаимоисключения на практике затрудняет расчеты и в некоторых случаях правило сегодняшней ценности перестает быть непогрешимым. В простейшем случае, когда существует постоянная ставка заимствования-кредитования (совершенный рынок капитала), кривая QV'V касается наивысшей из достижимых линий сегодняшней ценности в точке V', тогда как лучшей точкой на кривой QT'T является точка T'. Необходимо всего лишь рассмотреть обе точки, и та из них, которая располагается на самой высокой из достижимых линий сегодняшней ценности (в данном случае это точка T' на кривой QT'T), позволит инвестору достичь наивысшей из возможных кривых безразличия U1 в точке R. Напротив, посредством правила внутренней нормы дохода можно будет точно определить местонахождение T' и V', но нельзя будет провести различие между ними. Когда наблюдается разница в ставках заимствования и кредитования, как на рис. 2 (в настоящий момент геометрическое место точек производственных возможностей из этого рисунка следует интерпретировать как взаимно исключающие альтернативы), может возникнуть необходимость сопоставления, например, решения о кредитовании в точке V и решения о заимствовании в точке T. Чтобы обнаружить optimum optimorum, должны быть известны кривые безразличия (на рис. 2 оба эти решения позволяют достичь одной и той же кривой безразличия). Следует отметить, что сегодняшняя ценность не является здесь заслуживающим доверия ориентиром. В сущности, сегодняшняя ценность решения V (=W*) при норме дисконта, адекватной для нее (в качестве этой нормы выступает ставка кредитования), значительно превышает сегодняшнюю ценность решения T (= T*) при ее ставке дисконта (а эта ставка - ставка заимствования); хотя на самом деле оба эти показателя одинаковы. Допущение о возрастающих затратах, связанных с заимствованием, не создает дополнительных серьезных затруднений.
Другая форма отсутствия независимости (non-independence) вариантов, иллюстрируемая на рис. 6, также порождает трудности, неустранимые без модификации принципа определения оптимума. В данном случае проекты, расположенные вдоль геометрического места точек производственных инвестиций, не являются полностью независимыми, так как имеет место следующее ограничение: перед реализацией высокодоходных проектов нужно осуществить низкодоходные проекты. Опять-таки существует возможность нескольких локальных оптимумов типа V и T, которые можно сопоставлять вдоль одних и тех же линий на основе способа, описанного чуть выше.
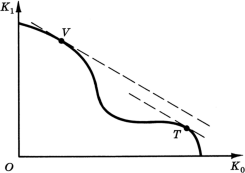 Рис.6. Взаимоисключающие инвестиционные возможности - осуществление низкодоходных проектов является предпосылкой для реализации высокодоходных проектов. |
6. Заключение для двухпериодного анализа
Решение задачи нахождения оптимальных инвестиций варьирует в зависимости от двух различных классификаций конкретных случаев. Первая классификация относится к способу, посредством которого рыночные возможности оказываются доступными для экономических субъектов; вторая классификация относится к отсутствию или наличию осложнений, связанных с взаимоисключением производственных возможностей. При использовании первой классификации простейшие, крайние, случаи суть следующие: а) совершенный рынок капитала (рыночные возможности таковы, что возможно кредитование и заимствование в любых количествах при одной и той же фиксированной ставке процента) и б) отсутствие каких-либо рыночных возможностей, как это имело место в ситуации Робинзона Крузо. Когда существует совершенный рынок капитала, общим множеством достижимых альтернатив является треугольник (рассматриваемый только в первом квадранте) типа OP'P на рис. 1, касающийся геометрического места точек производственных возможностей. Когда рынка капитала нет вообще, все множество достижимых альтернатив не что иное, как сама кривая производственных возможностей. Нетрудно видеть, каким образом различные формы несовершенства рынка капитала "находят свое место" между этими двумя крайностями.
Когда имеет место независимость физических (производственных) возможностей, последние могут быть проранжированы на основе убывания производственной нормы дохода. Если принято удобное (но несущественное) допущение непрерывности, то графически такая независимость означает, что геометрическое место точек производственных возможностей на всем своем протяжении вогнуто относительно начала координат, подобно QS'TV на рис. 1. Взаимоисключение альтернатив может иметь несколько форм (рис. 5, 6), но в каждом случае отсутствие тривиальной независимости вариантов означает, что кривая эффективных производственных возможностей не характеризуется простой вогнутостью. Это с очевидностью следует из рис. 6. На рис. 5 каждая из отдельных кривых производственных альтернатив, рассмотренная по отдельности, вогнута, но геометрическое место точек эффективных возможностей находится на наиболее выпуклых участках обеих кривых; иными словами, кривая эффективных производственных возможностей расположена вдоль линии QT'T снизу до точки X и от этой точки вверх по линии QV'V.
При использовании этой классификации можно представить подробную таблицу, иллюстрирующую различные оптимальные решения. Мы надеемся, что приводимое ниже краткое резюме общих принципов сможет почти полностью заменить такую таблицу.
1. Всегда, когда существует большое количество касаний кривых производственных возможностей и кривых полезности, что является нормальным следствием отсутствия независимости производственных альтернатив, правило внутренней нормы дохода оказывается неадекватным.
2. Правило сегодняшней ценности всегда работает в любых других ситуациях; кроме того, оно позволяет провести верное различие в оценках множества взаимоисключающих альтернатив при существовании совершенного рынка капитала (или же когда можно выявить и затем использовать для сопоставлений ставку дисконта, например когда касания кривых производственных возможностей и кривых полезности имеют место полностью в зоне I или же полностью в зоне III рис. 3).
3. Применение этих правил позволяет не ошибиться при определении оптимума только в формальном смысле, т. е. тогда, когда оптимальное решение содержит прямое касание кривой производственных возможностей и изокванты полезности, поскольку ставка дисконта, которую нужно знать для применения обоих правил, не что иное, как предельная ставка (норма) возможностей - продукт самого анализа.
4. Любые случаи, в которых даже принцип сегодняшней ценности может оказаться несостоятельным (привести к ошибочным ответам), отличаются двумя характеристиками: наличие большого количества касаний кривых производственных возможностей и изоквант полезности, вытекающее из отсутствия независимости инвестиций, и вдобавок отсутствие совершенного рынка капитала. Одним из важных примеров является сопоставление касания, связанного с заимствованием в зоне I, с касанием, связанным с кредитованием в зоне III. В таких ситуациях только обращение к карте полезности может дать правильные результаты.
5. Даже когда использование одного или обоих принципов позволяет безошибочно найти правильный результат не только в формальном смысле, ответ, который мы получаем в этом случае, - всего лишь производственное решение, представляющее собой только часть пути к достижению оптимума полезности. Более того, это производственное решение оптимально лишь тогда, когда можно допустить, что соответствующее финансовое решение будет фактически осуществлено.
II. Краткое замечание по поводу пожизненной ренты
Традиционный способ трактовки многопериодной ситуации в теории капитала заключался в рассмотрении инвестиционных решений как выбора между текущими фондами и бесконечными потоками будущего дохода. С точки зрения достижения некоторых целей это ценная идея, позволяющая упростить анализ. Однако ее нельзя здесь использовать, поскольку сущность практических трудностей, возникавших при принятии многопериодных инвестиционных решений, состоит в проблеме реинвестирования, т. е. в необходимости осуществления производственных или рыночных обменов между доходами различных будущих периодов времени. Вообще говоря, рассмотрение случая с пожизненной рентой - всего лишь вариант двухпериодного анализа, в котором существует одно-единственное настоящее и одно-единственное будущее. При изучении пожизненной ренты будущее удлиняется, но мы тем не менее не можем исследовать трансферты (дохода) между различными периодами этого будущего.
Все результаты, полученные в двухпериодном анализе раздела I, можно легко модифицировать для ситуации выбора между текущими фондами и пожизненной рентой. Вместо дохода K1 периода 1 (изображавшегося на рисунках) можно говорить о годовой норме роста дохода k. Кривые производственных возможностей и временных предпочтений будут характеризоваться почти теми же формами, что и прежде. Линии постоянной сегодняшней ценности (линии заимствования и кредитования) выражаются теперь уравнением C=K0+(k/i) вместо C=K0+K1/(1+i). Внутренняя норма дохода будет равна k/(-ΔK0). Оставшаяся часть анализа прямо вытекает отсюда, но я должен вместо ее изложения обратиться к рассмотрению более общего случая многопериодной ситуации.
III. Многопериодный анализ
Имеются большие сомнения относительно того, можно ли обобщить принципы двухпериодного анализа применительно к многопериодному случаю. Проблемы, затруднявшие анализ многопериодной ситуации, являются по сути результатом неудачных обобщений метода решения, которые приводят к неправильным выводам в упрощенном двухпериодном анализе.
1. Правило внутренней нормы дохода в сравнении с правилом сегодняшней ценности
При проведении многопериодного анализа не возникает формальных затруднений, связанных с обобщением кривых безразличий (представленных на рис. 1), которое превратило бы их в оболочки безразличия любого количества измерений. Можно также отметить, что все линии постоянной сегодняшней ценности, или рыночные линии, становятся гиперплоскостными; данное обстоятельство описывается следующим уравнением (его наиболее общей формой):


где С - параметр; i1 - норма дисконтирования дохода в период 1 по отношению к доходу в период 0; i2 - норма дисконтирования дохода в период 2 по отношению к доходу в период 1 и т. д.27 Если i1=i2=...=in=i, выражение принимает простой и более знакомый вид:
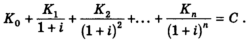
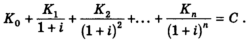
Главное затруднение при осуществлении многопериодного анализа возникает в процессе работы с третьим элементом решения, т. е. при описании производственных возможностей, которые можно обозначить f(K0, K1,...,Kn)=0. Однако проблема теоретической конкретизации оказывается не слишком трудной, если принять допущение о том, что все инвестиционные альтернативы независимы друг от друга. В сущности, проблема взаимоисключения в многопериодной ситуации не отличается от двухпериодной, и поэтому отказ от указанного допущения чрезмерно осложнит анализ. Тогда при этом условии и при принятии соответствующих предпосылок о непрерывности геометрическое место точек производственных возможностей можно рассматривать как кривую,28 вогнутую относительно начала координат во всех направлениях. Когда все приведенные допущения соблюдаются, между доходами в любые два периода Kr и Ks (при неизменности Kt во всех остальных периодах) будет иметь место пребывающее в двух измерениях геометрическое место точек, очень похожее на то место точек, что изображено на рис. 1.29
Теперь предположим, что могут иметь место кредитование или заимствование между двумя следующими один за другим периодами r и s по ставке is. Чтобы описать это графически, необходимо найти точку, аналогичную точке R' (рис. 1) в многомерном пространстве; такая точка будет располагаться на наивысшей линии сегодняшней ценности подобного пространства, достигаемой геометрическим местом точек производственных возможностей. При соблюдении простых допущений о вогнутости и непрерывности точка R' будет точкой касания. В результате этого возникнет дополнительное свойство, в соответствии с которым применительно к инвестиционным возможностям любой пары периодов (типа Kr и Ks) соотношение между предельными производственными нормами дохода, относящимися к Kr и Ks (при неизменности всех остальных K't), будет равно ставке дисконта между этими периодами. Далее, если это условие выполняется для всех пар периодов, следующих один за другим, оно будет точно так же соблюдаться для любых пар периодов.30 Опять-таки, как и в двухпериодном случае, окончательное решение будет связано с рыночным кредитованием или заимствованием (финансированием), осуществляемым для движения вдоль наивысшей гиперплоскости сегодняшней ценности, достигаемой при переходе от промежуточного производственного решения к оптимуму предпочтений в точке R. Следует отметить, что по сравнению с сегодняшней ценностью или прямым решением для соблюдения принципа уравнивания предельной производственной нормы дохода и ставки дисконта необходима предпосылка о непрерывности.
Именно здесь обращение к Фишеру, который, очевидно, сам понимал истинную сущность проблемы, может ввести в заблуждение. В своей "Ставке процента" он привел математическое доказательство, согласно которому оптимальное инвестиционное решение связано с соотношением, которое в нашем анализе описано как равенство между предельной производственной нормой дохода и рыночной процентной ставкой между любыми двумя периодами.31 Посредством очевидного обобщения результата двухпериодной проблемы этот принцип идентичен условию нахождения линии наивысшей сегодняшней ценности (двухмерной проекции гиперповерхности наивысшей сегодняшней ценности) между этими временными периодами. К сожалению, Фишер не смог осуществить последовательное раскрытие сути характеристики "между любыми двумя временными периодами" и в различных местах своей книги делает невразумительные утверждения о последствиях, к которым приведут инвестиции всегда, когда "норма дохода за жертву" или "норма дохода на затраты" между любыми двумя альтернативами превышает ставку процента.32
Теперь норма дохода за жертву при двухпериодных сопоставлениях эквивалентна производственной норме дохода. Однако для более общего случая Фишер определяет первый из этих показателей в многопериодном смысле; т. е., согласно его определению, норма дохода за жертву есть норма (ставка), которая сводит к нулевой сегодняшней ценности всю последовательность положительных и отрицательных периодических разниц между доходами по двум инвестиционным возможностям.33 В нашем контексте приведенное определение эквивалентно так называемой внутренней норме дохода.34 Однако, как будет продемонстрировано, использование этой нормы (которая будет обозначаться как ρ) приводит к неправильным (в общем случае) результатам, если процедура принятия или отрицания инвестиционных возможностей происходит на основе сопоставления ρ и рыночной ставки.35
2. Несостоятельность обобщенной внутренней нормы дохода
Кажется, что недавние рассуждения по поводу внутренней нормы дохода основаны на идеи обнаружения чисто внутреннего показателя временной производительности инвестиций, т. е. темпа роста капитальных фондов, вложенных в проект, для его сопоставления с рыночной ставкой (нормой).36 Но любая идея роста неизбежно означает соотношение и не может быть однозначна определена, если не известны величины (ценности) исходного и конечного состояний. Таким образом, инвестиционный проект, характеризующийся последовательностью годовых потоков наличности -1, 0, 0, 8, явно порождает темп роста, равный 100% (при ежегодном подсчете по методу сложных процентов), поскольку такой проект фактически сводится к двухпериодному проекту с промежуточным начислением на основе метода сложных процентов. Аналогичным образом сберегательный вклад в 10% годовых, ежегодно начисляемых по методу сложных процентов в течение n лет, может показаться многопериодным проектом; но правильно он трактуется в качестве последовательности двухпериодных проектов (рост будет иметь место, только если в начале каждого периода принимается решение реинвестировать сумму капитала и процента, заработанного инвестициями предыдущего периода). Проект, связанный с помещением денег на сберегательный счет без реинвестиций, приносил бы такую последовательность доходов: -1, 0.1, 0.1, 0.1,..., 1.1 (последний элемент представляет собой окончательную выплату); при реинвестициях эта последовательность становится следующей: -1, 0, 0, 0,..., (1.1)n, где n - число периодов начисления сложных процентов, прошедших после помещения в банк исходного вклада.
Однако рассмотрим более обычный инвестиционный проект, приносящий последовательность выплат -1, 2, 1. (Вообще говоря, все рассмотренные здесь инвестиционные альтернативы, можно стандартизировать, допустив, что исходные затраты или поступления равны 1 дол.). Каким образом можно определить темп роста исходных капитальных расходов? В отличие от альтернативы, связанной с помещением средств на сберегательный счет, отсутствует информация, касающаяся нормы, по которой может происходить реинвестирование промежуточных поступлений, составляющих 2 дол. Конечно, если мы применим какую-то внешнюю норму дисконтирования (например, стоимость капитала или ставку, по которой можно оценить внешние кредитные возможности), то мы тем самым откажемся от идеи чисто внутренней нормы роста. По сути, использование внешней нормы (ставки) означает просто-напросто не что иное, как оценку инвестиционных проектов на основе принципа сегодняшней ценности.
При попытках устранить это затруднение Фишером и его последователями было отобрано для обобщения одно из математических свойств двухпериодной предельной производственной нормы дохода. Это свойство, в сущности, состоит в том, что, когда ρ (в двухпериодной ситуации равное предельной производственной норме дохода ΔK1/(-ΔK0)-1 употребляется для дисконтирования ценностей потока поступлений-платежей, дисконтированная ценность становится нулевой. Данное обстоятельство само по себе позволяет нам легко сделать следующее обобщение: для любого многопериодного потока будет существовать подобная норма дисконтирования ρ, которая приравнивает дисконтированную ценность нулю (по крайней мере таково было предположение указанных выше экономистов). Возникает впечатление, что эта норма - чисто внутренняя, не подверженная какими-либо рыночными влияниями. И в определенных простых случаях ее использование позволяет сделать правильный выбор среди инвестиционных проектов согласно принципу: соглашайся на реализацию проекта, если ρ больше, чем рыночная ставка r.
Для рассмотренного выше инвестиционного проекта с потоком -1, 2, 1 ρ равна √2 или 141.4%. И, в сущности, если ставка заимствования или ставка по наилучшей альтернативной возможности (нужно выбрать ту из них, которая в данном случае лучше всего подходит для сравнения) меньше √2, инвестиции желательны. На рис. 7 изображена сегодняшняя ценность С проекта в виде функции дисконтированной процентной ставки i при допущении неизменности последней в течение двух дисконтируемых периодов. Следует отметить, что сегодняшняя ценность проекта уменьшается по мере роста i на всем протяжении диапазона процентных ставок от i=-1 до i=∞ .37 Внутренняя норма дохода ρ - такая i, при которой кривая сегодняшней ценности пересекает горизонтальную ось. Очевидно, что для любых i<ρ сегодняшняя ценность больше нуля; для i>ρ она отрицательна.
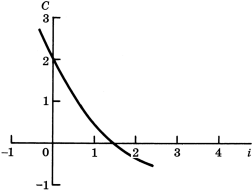 Рис.7. Кривая сегодняшней ценности проекта, связанног с потоком -1, 2, 1. |
Однако то обстоятельство, что использование ρ позволяет принять правильное решение в конкретном случае или типе случаев не означает, что оно является верным по существу. И действительно, можно привести примеры, когда применение этого показателя приводит к ошибочным результатам. Алчиан показал, что при сопоставлении двух альтернативных инвестиционных проектов выбор проекта с более высоким ρ не является оптимальным в общем случае; в действительности решение не может быть принято без наличия информации о соответствующей внешней норме дисконтирования.38 Рис. 8 иллюстрирует два таких проекта; проект I предпочтительнее при низких процентных ставках, а проект II - при высоких. Ставка i, при которой они предпочтительны в равной степени, - фишеровская норма дохода за отказ от одного проекта в обмен на другой. Но проект II имеет более высокую внутреннюю норму дохода (т. е. его сегодняшняя ценность падает до нуля при более высокой норме дисконтирования) независимо от фактической процентной ставки. Как же тогда мы можем говорить, что проект I выгоднее при низких процентных ставках? Поскольку его сегодняшняя ценность выше, она позволяет инвестору двигаться вдоль наивысшей гиперповерхности для обнаружения оптимума полезности, лежащей где-то на этой гиперповерхности. Если бы был принят проект II, инвестор также получил бы возможность перемещаться вдоль такой гиперповерхности, но последняя была бы расположена ниже. Возможен еще один образ действий (при определенной низкой процентной ставке): инвестор, выбравший первоначально проект I, мог бы при желании заполучить поток наличности, порождаемый проектом II, посредством соответствующих действий по заимствованию и кредитованию, сопровождаемых потерей части богатства.39
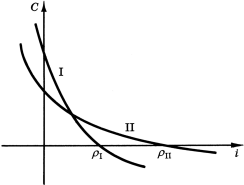 Рис.8. Два альтернативных проекта. |
Существует еще более фундаментальный аспект: Лори и Сэвидж показали, что ρ может не иметь единственного значения.40 Рассмотрим, например, инвестиционный проект с таким потоком: -1, 5, -6. Расчеты показывают, что этот проект имеет нулевую сегодняшнюю ценность при ставке процента, равной как 100, так и 200%. Функция сегодняшней ценности этого проекта от нормы дисконтирования изображена на рис. 9. Хотя Лори и Сэвидж говорили только о "двойных" внутренних нормах дохода, в принципе возможно любое количество нулевых сегодняшних ценностей. Например, проект, приносящий поток наличности -1, 6, -11, 6 - он проиллюстрирован на рис. 10 - характеризуется нулевой сегодняшней ценностью при нормах дисконтирования, равных 0, 100 и 200%.41
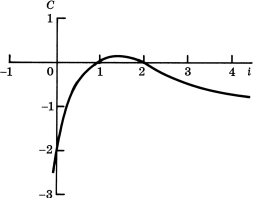 Рис.9. Кривая сегодняшней ценности инвестиционного проекта, приносящего поток наличности. |
В сущности, абсолютно приемлемые инвестиционные проекты могут отличаться отсутствием настоящих внутренних норм (в такой ситуации уравнение сегодняшней ценности имеет только мнимые корни). В качестве примера можно привести проект, приносящий поток -1, 3, -2.5; график функции сегодняшней ценности такого проекта покажет, что этот показатель меньше нуля на всем протяжении допустимого диапазона.42 Однако с определенностью нельзя утверждать, что все проекты, у которых нельзя вычислить внутреннюю норму дохода, являются плохими. Если мы в только что рассмотренном проекте всего лишь поменяем знаки элементов потока наличности на противоположные, получив 1, -3, 2.5, то мы будем иметь проект с положительной сегодняшней ценностью при всех ставках дисконта.
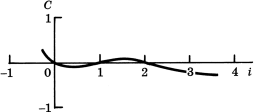 Рис.10. Кривая сегодняшней ценности инвестиционного проекта, приносящего поток наличности -1, 6, -11, 6. |
Эти примеры несостоятельности правила внутренней нормы дохода в многопериодной ситуации (здесь следует отметить, что в каждом из рассмотренных случаев принцип сегодняшней ценности продолжает четко давать правильный ответ, если абстрагироваться от проблемы наличия соответствующей нормы дисконтирования, проанализированной в разделе I) являются, конечно же, симптомами лежащей в основе этого правила ошибочной концепции. Ясно, что идея, согласно которой ρ представляет собой рост в любом смысле этого слова, не может быть верной; ценность капиталовложений, равных 1 дол., не может возрастать с темпом как в 100, так и в 200%. Более того, точка зрения, в соответствии с которой ρ - исключительно внутренняя норма, также неправильна. Давайте рассмотрим проанализированный ранее проект -1, 2, 1 с единственным ρ, равным 2. Доход в 2 дол., получаемый в промежуточный период, должен быть, несомненно, реинвестирован вне этого проекта. Как при расчете ρ учесть данное обстоятельство? Ответ заключается в следующем. При проведении связанных с вычислением ρ математических преобразований неявно допускается, что все промежуточные платежи - как положительные, так и отрицательные - трактуются так, как будто они начисляются по формуле сложных процентов с темпом, равным ρ.43 Норма ρ характеризовалась скорее как "ставка нахождения" (solving rate) процента. Но нужно отметить, что такое математическое преобразование, даже когда оно приводит к единственному ответу (а в общем и целом этого не происходит), является неприемлемым с точки зрения вытекающего из него экономического смысла. В обычной ситуации не будет ни альтернативных инвестиционных вариантов для вложения (по норме ρ) дохода, заработанного в промежуточный период, ни получения за счет заимствования (по этой же норме ρ) потоков наличности в тот же самый промежуточный временной интервал. Норма ρ, являющаяся следствием математического преобразования, только в случаях редких совпадений будет отражать реальные экономические альтернативы.
В приведенных выше аргументах против использования обычного понятия "внутренняя норма дохода" не учитывается как-либо возможность изменения процентных ставок с течением времени. Мартин Дж. Бэйли обратил мое внимание на то, что когда это действительно имеет место (т. е. когда существует известная динамика будущих изменений i), правило внутренней нормы дохода оказывается еще более несостоятельным. Ведь при употреблении этого правила все временные периоды трактуются как одинаковые; единственным дисконтирующим фактором является "ставка нахождения", определяемая только в виде последовательности потоков наличности. Но при (известной динамики) изменениях будущего i возникают перемены в относительной желательности доходов различных периодов. При обычном изложении концепции внутренней нормы дохода данное обстоятельство не учитывается. В действительности в таком случае можно осуществить инвестиции, для которых ρ четко и однозначно определено, но при этом нельзя определить желательность альтернативных возможностей (т. е. в зависимости от временной структуры будущих процентных ставок сегодняшняя ценность может быть положительной или отрицательной).
В приводимых ниже замечаниях я попытаюсь обобщить основные принципы, изложенные в этом разделе.
По меньшей мере в простейшей ситуации, в которой нам не нужно думать о разнице между ставками заимствования и кредитования, и принимается допущение об их равенстве и постоянстве (постоянстве по отношению к объемам займов или кредитов, а не во времени), многомерное решение является простым обобщением двухпериодного решения. Принцип нахождения оптимума временных предпочтений заключается в доведении производственных инвестиций до точки, в которой достигается наивысший из достижимых уровней сегодняшней ценности, и последующем "финансировании" этих инвестиций за счет заимствования или кредитования между временными периодами.
Основная тема нашего анализа касалась нереалистичности обобщения правила внутренней нормы дохода - в отличие от правила сегодняшней ценности - применительно к многопериодной ситуации, если при этом принимается стандартное определение внутренней нормы ρ, т. е. если предполагается, что это норма, при которой сегодняшняя ценность дисконтированного потока доходов становится равной нулю. Я пытался показать такое многопериодное обобщение, которое все же сохранит правильность принципа внутренней нормы дохода: между каждой парой периодов времени предельная внутренняя норма дохода (т.е. предельная производственная норма дохода между этими двумя периодами при постоянстве дохода других периодов) должна быть установлена равной рыночной ставке дисконта между данными периодами. Обычная интерпретация правила внутренней нормы дохода в общем не является правильной - этот факт иллюстрируется его несостоятельностью в конкретных случаях и объясняется его зависимостью от неявной предпосылки, делаемой при математическом преобразовании, посредством которого определяется ρ. В соответствии с этой предпосылкой все промежуточные потоки наличности реинвестируются (или берутся взаймы, если они меньше нуля) с темпом, равным ρ. Вдобавок, допускается неизменность межпериодных норм предпочтения (или процентных ставок) с течением времени. Поэтому рассмотренная обобщенная многопериодная внутренняя норма дохода в действительности не является внутренней; более того, с учетом принимаемой предпосылки относительно внешних возможностей эта норма, вообще говоря, не только неправильна, но даже экономически бессмысленна.
IV. Заключительные комментарии
В проведенном анализе не было уделено внимания очень большому числу проблем. Вдобавок из-за недостатка времени пришлось отказаться от сравнительного анализа работ других авторов, который мог бы оказаться весьма полезным.44
Я не пытался обобщать результаты, получающиеся в многопериодной ситуации при взаимозависимости инвестиций или при разнице между ставками заимствования и кредитования или их непостоянстве. Относительно последних двух аспектов интуиция подсказывает, что факт использования или неиспользования ставок заимствования и кредитования при вычислении сегодняшней ценности в любом периоде не зависит от каких-либо характеристик инвестиционных проектов, рассмотренных отдельно. Это зависит скорее от общей ситуации с наличностью после принятия конкретного проекта в качестве прироста. Если после такого принятия временные предпочтения диктуют уменьшить доход в период r и увеличить его в период t, то любой доход периода r, связанный с рассматриваемым проектом, должен быть дисконтирован "назад" до предыдущего периода по ставке кредитования (и до периода t по ставке заимствования). Доход любого периода s можно затем последовательно дисконтировать по ставкам заимствования в течение ряда одних периодов и по ставке кредитования в течение ряда других периодов прежде, чем он будет сведен к сегодняшней ценности.
Основной положительный вывод данной статьи состоит в том, что принцип сегодняшней ценности при принятии инвестиционных решений является правильным в большом количестве разных случаев (но не во всех), однако в то же время не полным. Это правило позволяет нам достичь наивысшего возможного уровня сегодняшней ценности; но точка, в которой данное условие удовлетворяется (т. е. в которой имеет место наилучшее распределение доходов в различные периоды), не является точкой окончательного решения. Она представляет собой, скорее, точку промежуточного производственного решения, которое затем должно быть модифицировано за счет заимствования или кредитования ("финансирования") для нахождения полного оптимума. Это становится особенно ясным при рассмотрении случая, в котором ставки кредитования и заимствования различны; здесь мы включились в полемику между теми, кто отдает предпочтение дисконтированию сегодняшней ценности по стоимости капитала, и теми, кто выступает за ее дисконтирование по альтернативной ставке кредитования. Правильность какого-либо из этих подходов зависит от способа финансирования, необходимого для приближения к оптимуму временных предпочтений. Далее, если касание между геометрическим местом точек производственных возможностей и изоквантой полезности (временных предпочтений) происходит при норме, которая находится между ставками кредитования и заимствования (больше первой и меньше второй из них), то производственное решение не требует финансирования,и принцип сегодняшней ценности оказывается правильным лишь в формальном смысле. На основе употребления этого принципа нельзя получить правильный ответ только в определенных случаях, в которых имеет место сочетание затруднений, порождаемых взаимозаменямостью инвестиций, и отсутствия совершенного рынка капитала. При наличии последнего принцип сегодняшней ценности является правильным всегда, но при этом все равно остается неполным (об этой неполноте было сказано чуть выше). При независимости инвестиций, имеющей место, однако, при несовершенном рынке капитала, посредством применения данного правила можно получить ответы, которые верны, но, возможно, только в формальном смысле (т. е. используемая ставка дисконтирования является не внешней нормой, а внутренней теневой ценой, которая выводится из анализа).
Основной отрицательный вывод состоит в том, что применение правила внутренней нормы дохода в многопериодной ситуации в общем и целом дает неправильные результаты, если принимается обычное определение этой нормы; согласно данному определению, внутренняя норма - это ставка, приравнивающая нулю сегодняшнюю ценность потока доходов, порождаемого инвестиционным проектом. Так называемая внутренняя норма позволяет получать правильные ответы, только если ее использование ограничено двухпериодными сопоставлениями; я назвал такую двухпериодную внутреннюю норму производственной нормой дохода. При употреблении для оценки многопериодных инвестиций стандартное правило внутренней нормы дохода (состоящее в сравнении ρ с рыночной ставкой r) дает, как правило, неверные результаты; однако при определенных предпосылках о непрерывности можно получить правильный ответ, установив предельную производственную норму дохода между каждой парой временных периодов, равной ставке дисконта или рыночной ставке между этими же периодами.
Более важным, чем конкретные детальные выводы, является доказательство того, что фишерианский подход - анализ инвестиционных решений как средства балансирования потребительских доходов во времени, осуществляемый при условии различения между производственными и рыночными инвестиционными возможностями, - позволяет решить (теоретически) все поставленные проблемы. Следует далее отметить, что такое решение - не "нарост" на общей экономической теории выбора, но полностью интегрировано в нее, будучи, так сказать, ее дополнительным измерением. Экономисты, работавшие в области теории инвестиционных решений после Фишера, придерживались механистического подхода - одни выступали за использование этой формулы, другие - за использование той формулы, и т. д. С фишеровской точки зрения, мы можем видеть, что ни одна из предлагавшихся до сих пор формул не является приемлемой во всех без исключения случаях. Более того, даже когда, например, принцип сегодняшней ценности позволяет получить правильные результаты, мало кто понимает, что его правильность обусловлена принятием финансовых решений, как это демонстрируется в фишеровском анализе. Короче говоря, фишеровский подход дает нам возможность определить диапазон применимости и недостатки всех предлагаемых формул, тем самым закладывая основу для общего теоретического решений проблемы инвестиционных решений в условиях определенности.
ПРИМЕЧАНИЯ:
i Опубликовано в "Journal of Political Economy" (1958. Vol. 66. Aug. P. 329-352).
1 Выражаю признательность многим из моих коллег, и особенно Джеймсу Лори и Мартину Бэйли, за ценные предложения и критику.
2 Наиболее известна следующая книга: Fisher I. The Theory of Interest. New York : Macmillan, 1930. Большинство основных идей содержится в его ранней работе: Fisher I. The Rate of Interest. New York : Macmillan, 1907.
3 Вклад Фишера в теорию капитала связан далеко не только с его решением проблемы, анализируемой в этой статье, - проблемы определения оптимальных инвестиций. Он также рассматривал вопрос о равновесии на рынке капитала, балансирующем предложение и спрос всех принимающих решения субъектов.
4 В статье не проводится различие между индивидами и фирмами. Последние рассматриваются лишь как учреждения или инструменты индивидов.
5 Наклон рыночной линии равен, конечно же, -(1+i), где i - ставка заимствования-кредитования. Иными словами, когда кто-то отдает 1 дол. в период 0 и получает в обмен (1+i) дол. в период 1.
6 На данной стадии анализа лучше избегать термина "внутренняя норма дохода". Фишер использует выражения "норма дохода за жертву" или "норма дохода по затратам".
7 Индивид, находящийся изначально в точке S', будет также иметь возможности дезинвестиций.
8 Правило сегодняшней ценности - более или менее стандартный принцип, предлагаемый очень многими теоретиками. Правило внутренней нормы дохода в том смысле, в котором оно здесь используется, также часто выдвигалось (см., например: Dean J. Capital Budgeting. New York : Columbia University Press, 1951. P. 17-19). Ссылки на использование альтернативных инвестиционных критериев можно найти в следующей работе: Lutz F., Lutz V. The Theory of Investment of the Firm. Princeton, N. J. : Princeton University Press, 1951. P. 16. Правило внутренней нормы дохода, которую мы будем детально рассматривать (т. е. мы учтем все проекты и приращения их стоимости, для которых внутренняя норма дохода превышает рыночную процентную ставку), отличается от аналогичного правила, анализируемого Лутцами (они рассматривают временную структуру инвестиций, максимизирующих внутреннюю норму дохода). Правило, рассматриваемое здесь, позволяет сопоставлять приростную или предельную норму дохода с рыночной процентной ставкой; в других теориях максимизируется средняя норма дохода без учета рыночной ставки. Будет показано, что второе правило является фундаментально неверным, даже в той форме, в которой его используют Лутцы в качестве окончательного критерия (в их концепции максимизируется внутренняя норма дохода на собственный капитал инвестора). Данный аспект будет анализироваться ниже, в разделе 4, в связи с рационированием капитала.
9 Действительно, для двухпериодной ситуации эти правила идентичны: можно показать, что любой проект (или прирост его стоимости) с положительной сегодняшней ценностью будет иметь внутреннюю норму дохода, превышающую рыночную процентную ставку.
10 Если бы ставка заимствования была ниже ставки кредитования, то была бы возможность накопления неограниченных размеров богатства за счет займов с последующим ссужением; поэтому я не рассматриваю эту возможность. Конечно, финансовые институты обычно в среднем берут взаймы по ставке, которая ниже той, по которой они дают кредиты; однако они не могут расширить объем своих операций неограниченно, не изменив данное соотношение.
11 Предельная норма производственных возможностей, или предельная внутренняя норма дохода, измеряет норму дохода по наилучшему альтернативному проекту. При допущении непрерывности эта норма дохода определяется наклоном линии QRQ' в точке R на рис. 3. Очевидно, что касание линии сегодняшней ценности U1 и QRQ' в точке R будет (алгебраически) означать правильность принципа сегодняшней ценности. И сопоставление этой нормы с предельной внутренней нормой дохода по мере изменения последней вдоль QRQ' будет означать алгебраическую (формальную) правильность и второго принципа - внутренней нормы дохода.
12 Ставка заимствования ("стоимость капитала") рекомендовалась Дином, а также Лори и Сэвиджем (Dean J. Capital Budgeting. Esp. p. 43-44; Lorie J. H. Savage, L. J. Three Problems in Rationing Capital // Journ. Business. 1955. Vol. 28. O. A. P. 229-239, esp. p. 229). Робертс и Лутцы выступают за использование ставки кредитования (Lutz F., Lutz V. The Theory of Investment... Esp. p. 22; Roberts H. V. Current Problems in the Economics of Capital Budgeting // Journ. Business. 1957. Vol. 30. Jan. P. 12-16).
13 Я должен поблагодарить Джоэла Сигелла за акцентирование внимания на данном аспекте при обсуждении этой проблемы. Следует отметить, что ставка, представляющая собой предельные затраты, связанные с заимствованием, не обязательно ставка заимствования по предельным фондам, поскольку прирост величины займов может увеличить ставку по допредельным (infra-marginol) единицам.
14 Хотя данная точка зрения может быть доказана геометрически, она прямо следует из аналитических свойств огибающей кривой.
В целях упрощения обозначений в данном примечании я буду трактовать K1 на рис. 4 как y и K0 как x. Тогда уравнение геометрического места точек производственных возможностей можно записать следующим образом:
y0=f(x0). (1)
Семейство рыночных кривых может быть выражено как y-y0=g(x-x0) или
F(x,x0)=f(x0)+g(x-x0). (2)
Огибающая линия, y=h(x), определяется условием, согласно которому любая точка на ней должна быть точкой касания с некоторым семейством кривых (2). Таким образом, мы имеем
h(x)=F(x,x0), (3)


Второе условие огибающей линии заключается в том, что частная производная функции (2) по отношению к ее параметру должна равняться нулю:


Но
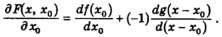
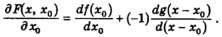
Отсюда
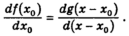
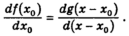
Также
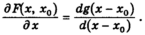
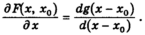
Наконец
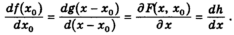
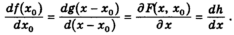
Таким образом, наклон геометрического места точек производственных возможностей равен наклону огибающей линии в точках, в которых эти две кривые соединяются одной и той же рыночной кривой.
15 Выражение "рационирование капитала" использовалось некоторое время назад Хартом применительно к неценовым ограничениям на долговое или акционерное финансирование (Hart A. G. Anticipations. Business Planning, and the Cycle // Quart. Journ. Econ. 1937. Vol. 60. P. 273-297). Он не употреблял этот термин имея в виду доступное фиксированное количество капитала; в контексте его работы данный термин можно интерпретировать, в сущности, просто как фактор возрастания предельных затрат на приобретение капитальных фондов. См. также: Dean J. Managerial Economics. Englewood Cliffs, N. J. : Prentice-Hall, Inc., 1951. P. 586-600. В значении фиксированной величины фондов этот термин использовался различными авторами, обсуждавшими проблемы деятельности предприятий или правительства (см.: Margolis J. The Discount Rate and the Benefits-Cost Justification of Federal Irrigation Investment. Stanford, Calif., 1955; Lorie J. H., Savage L. J. Three Problems...; McKean R. Efficiency in Government through Systems Analysis. New York : John Wiley & Sons, 1958).
16 Scitovsky T. Welfare and Competition. Chicago : Richard D. Irwin, Inc., 1951. P. 208-209.
17 Lutz F., Lutz V. The Theory of Investment... P. 16-48, esp. p. 17, 20, 42.
18 Scitovsky T. Welfare... P. 194.
19 Скитовски отказывается от приемлемого аргумента в ранней части своего анализа, согласно которому готовность ссужать и брать в долг является неограниченной, в пользу неприемлемой точки зрения в поздней части анализа, в соответствии с которой текущие капитальные фонды фиксированы (Scitovsky T. Welfare... P. 193-200, 208-209).
20 Lutz F., Lutz V. The Theory of Investment... P. 3-13.
21 Возможно, однако, что Лутцы имели в виду только случай, в котором инвестор начинает свою деятельность, не имея, кроме текущих фондов, других активов. В этой ситуации при определении величины собственного капитала не возникает проблемы дисконтирования, так что в таком контексте их конечный критерий нельзя критиковать. Однако возражение, выдвигаемое ниже по отношению к критерию Скитовски, состоящее в том, что этот критерий не учитывает альтернативы, связанные с потреблением, которые относятся к самой сути проблемы инвестиционных решений, будет затем применено и к правилу Лутцев. Вдобавок принцип, согласно которому инвестор обладает только текущими фондами, вряд ли является настолько общим, что его можно применить при определении окончательного критерия. Лутцы сами признают возможность ситуации, при которой инвестор не имеет в собственности капитала, но использует только заемные фонды; и применительно к этой ситуации они сами отказались от окончательного критерия (Lutz F., Lutz V. The Theory of Investment... P. 42. Note 32). В самом общем случае, конечно же, инвестор имеет диапазон производственных возможностей, которые могут принести ему альтернативные сочетания сегодняшнего и будущего доходов.
22 Следуя уже изложенным принципам, мы могли бы без больших затруднений найти оптимум в ситуации, при которой заимствование разрешено, но лишь в определенных фиксированных лимитах. Эффектом такого ограничения явилось бы появление огибающей кривой достижимости, похожей на аналогичную кривую на рис. 4, но несколько иной формы.
23 Scitovsky I. Welfare... P. 209.
24 Это точка Q' на рис. 3. Такой итог, конечно же, тривиален. Скитовски, возможно, имел в виду выбор среди инвестиционных возможностей, не являющихся независимыми друг от друга (этот аспект рассматривается в следующем разделе); в подобной ситуации каждая инвестиционная альтернатива может иметь свою особую точку пересечения с осью K1. Здесь мог бы быть сделан нетривиальный выбор средней нормы дохода в качестве критерия максимизации.
25 Возможно, Скитовски подразумевал ситуацию, при которой определенная доля текущих фондов K0 изымается из сферы потребления (на некоторой неизвестной основе), чтобы стать фиксированными текущими капитальными фондами. В этом случае ситуация Скитовски приведет к верному результату, если бульшая величина фиксированных капитальных фондов будет распределена таким образом, что инвестор достигнет точки R' на своем геометрическом месте точек производственной трансформации (описанной на рис. 3).
26 Можно было бы, конечно, свести анализ к исходной простоте, но только в том случае, если бы одно геометрическое место точек находилось полностью внутри другого - это означало бы, что первое из них, очевидно, характеризуется более низким качеством и может быть опущено при рассмотрении.
27 В этом разделе я не собираюсь далее рассматривать возможные расхождения между ставками кредитования и заимствования (подробно исследованные в разделе I); я буду просто говорить о ставке дисконта (норме дисконтирования), или рыночной ставке. Эти принципы существенно не изменяются в многопериодной ситуации; мне бы хотелось сосредоточить внимание на некоторых других затруднениях, тех, что возникают, когда количество периодов превышает два. Можно отметить, что в самом общем случае предпосылка полной информации становится весьма нереалистичной - я имею в виду предпосылку, согласно которой временная структура процентных ставок от i1 до in известна сегодня.
28 Как и в двухпериодном случае, геометрическое место точек описывает не все производственные возможности, но лишь границу области, представленной производственными возможностями. Граница состоит из тех возможностей, над которыми не доминируют (т. е. не являются более хорошими) другие альтернативы; любая возможность, изображенная точкой, находящейся внутри границы, хуже, чем по меньшей мере одна альтернатива (последняя описана точкой, лежащей на границе).
29 Допущение n-мерной непрерывности труднее признать реалистичным, чем двухмерную непрерывность. Тем не менее такое несоответствие реальности несущественно; при этом данное допущение сильно облегчает изложение модели. Следует упомянуть одну из возможных ошибочных интерпретаций обсуждаемой предпосылки о непрерывности: эта предпосылка не обязательно означает, что единственные рассматриваемые инвестиционные возможности - двухпериодные альтернативы "между" парами периодов в настоящем или будущем. Подлинные многопериодные возможности допустимы; в качестве примера можно привести альтернативу, описываемую потоками наличности, равными -1, +4, +2 и +6 соответственно в периоды 0, 1, 2 и 3. Скорее, предпосылка непрерывности означает, что, если мы хотим отказаться от альтернативы, подобной только что приведенной, в пользу возможности, дающей больше дохода в период 1 и меньше дохода, скажем, в период 3, мы можем найти другие доступные альтернативы, например как эта: -1, +4+ Ε1, +2, +6-Ε3, где Ε1 и Ε3 - бесконечно малые величины. Иными словами, пребывая в любой точке, относящейся к геометрическому месту точек производственных возможностей, можно непрерывно осуществлять обмены между доходами в любых парах периодов.
30 Максимизируя лагранжиан, C-λf(K0, K1,...,Kn) мы получим условия первого порядка:
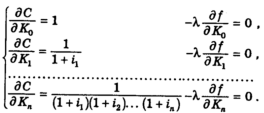
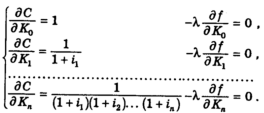
Элинируем λ между любыми двумя периодами, следующими один за другим:
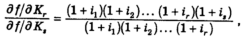
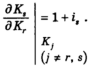
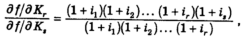
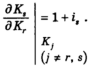
А теперь сделаем то же самое между периодами, не следующими один за другим:
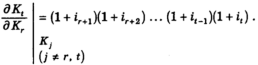
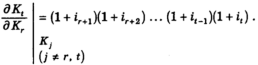
31 Fisher I. The Rate of Interest. P. 398-400. Фактически доказательство касается только последовательных периодов, но это ограничение несущественно.
32 Fisher I. : 1) Rate of Interest. P.155; 2) Theory of Interest. P. 168-169.
33 Fisher I. Rate of Interest. P.153; 2) Theory of Interest. P. 168-169.
34 Ради некоторых целей важно провести различие между ставкой, на основе которой сегодняшняя ценность потоков поступлений от инвестиций сводится к нулю, и ставкой, на основе которой делается то же самое применительно к потокам разниц между поступлениями от двух альтернативных инвестиционных проектов (см.: Alchian A. A. The Rate of Interest, Fisher's Rate of Return over Cost, and Keynes' Internal Rate of Return // Amer. Econ. Rev. 1955. Vol. 45. Dec. 1955. P. 938-943). Ради текущих целей нет нужды делать такое различие, поскольку индивидуальные инвестиционные возможности трактуются как независимые приращения; так что поступления от инвестиционных проектов, о которых идет речь, являются, по сути, последовательностью разниц между потоками двух величин, одна из которых возникает в случае принятия данного проекта, а другая - в случае его отвержения.
35 При еще одном усложнении в фишеровской математической модели сопоставляются двухпериодные предельные нормы дохода за жертву со ставками процента между двумя рассматриваемыми периодами, причем не допускается неизменность этих ставок. При изучении многопериодной ситуации Фишер нигде не указывает, как превратить различающиеся от периода к периоду процентные ставки во всеобщую рыночную ставку для ее сравнения с ρ. Возможно, что в этом пункте анализа Фишер думал лишь о процентной ставке, остающейся постоянной во времени; тогда только что указанный вопрос не возникает. Затруднения, связанные с использованием внутренней нормы дохода при изменениях рыночной ставки в времени, будут рассматриваться ниже.
36 См. Boulding K. E. Economic Analysis. New York : Harper & Bros 1948. P. 819.
37 Экономические рассуждения могут быть применимы к отрицательным процентным ставкам; такие ставки будут нормой сокращения капитала. Однако я не допускаю возможности, при которой ставка сокращения капитала превышает 100%.
38 Alchian A. A. The Rate of Interest... P. 939.
39 Некоторым будет так трудно с этим согласиться, что я должен привести числовой пример. Пусть инвестиционный проект I порождает годовой поток наличности -1, 0, 4; тогда внутренняя норма дохода равна 1, или 100%. Пусть также проект II приносит тот же поток денег, что и инвестиции, проиллюстрированные на рис. 7: -1, 2, 1. Этот проект характеризуется внутренней нормой дохода, равной √2 или 141.4%. Таким образом, внутренняя норма дохода проекта II больше. Однако сегодняшняя ценность проекта I более высока при нулевой процентной ставке и, в сущности, такое соотношение не меняется, пока не достигается ставка, при которой кривые сегодняшних ценностей обоих проектов пересекаются. Такое пересечение имеет место при процентной ставке, равной 50%. Теперь мы можем легко продемонстрировать, как, выбирая изначально проект I, можно в конечном счете получить результат, порождаемый проектом II при любой ставке процента ниже 50%, например при 10%-й ставке. Осуществляя заем таким образом, что доход конечного периода падает, а промежуточного периода растет, мы конвертируем поток наличности -1, 0, 4 в поток -1, 2.73, 1 (я вычел из дохода последнего периода 3 и прибавил эту величину к доходу промежуточного периода следующим образом: 3 : 1.1 = 2.73). Мы теперь можем получить проект II, отняв 0.73, ведь тогда поток доходов будет равен : -1, 2, 1. Факт, состоящий в том, что мы имеем возможность получить проект II, потеряв некоторый объем богатства, демонстрирует превосходство проекта I, имеющее место даже несмотря на ρII > ρI при условии, согласно которому заимствование и кредитование могут иметь место при процентной ставке, меньшей, чем дисконтирующая норма 50% (при которой пересекаются кривые сегодняшней ценности обоих проектов).
40 Lorie J. H., Savage L. J. Three Problems... P. 236-239.
41 Примеры, рассмотренные выше, показывают, что изменение знаков в потоках поступлений каким-то образом влияет на возможность появления множества ρ. В сущности, декартово правило знаков показывает нам, что количество решений в допустимом диапазоне (количество точек, в которых сегодняшняя ценность равна нулю при i>-1) может быть равно (самое большее) количеству решений с обратным знаком; перемена знака относится к значениям элементов потока наличности. Поэтому двухпериодный инвестиционный проект может характеризоваться не более чем одной ρ, трехпериодный проект - не более чем двумя ρ и т. д. Существует интересное примечание в одной из работ Фишера, где утверждается, что он не был полностью неосведомлен о данном затруднении. Для случаев, в которых имеет место изменение как минимум двух знаков, он рекомендует использование метода сегодняшней ценности, а не попытку расчета "нормы дохода за отказ" (Fisher I. Rate of Interest. P. 155). Возможность существования какого угодно количества нулевых значений функции сегодняшней ценности была отмечена Полом Э. Самуэльсоном (p. 475) в следующей статье: Samuelson P. A. Some Aspects of the Pure Theory of Capital // Quart. Journ. Econ. 1936-1937. Vol. 60. 469-496.
42 Алгебраически формула корней трехпериодного проекта, приносящего поток наличности n0, n1, n2, где n0=-1, выглядит следующим образом:
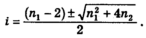
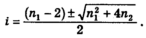
Если -4n2 превышает n21, корни будут мнимыми и внутреннюю норму дохода нельзя будет рассчитать. Необходимым условием существования полученного результата является отрицательное значение суммы недисконтированных потоков наличности; однако наличие этого условия не должно исключать рассмотрение проекта (обратите внимание на проект -1, 5, -6, показанный на рис. 9).
43 Истинное значение предпосылке о реинвестициях было выявлено таким экономистом, как Эзра Соломон (Solomon E. The Arithmetic of Capital-budgeting Decisions // Journ. Business. 1956. Vol. 29. Apr. P. 124-129, esp. p. 126-127.
44 Хотя мне бы хотелось прокомментировать важную статью Самуэльсона (Samuelson P. A. Some Aspects...) Результаты, полученные в этой работе, отчасти совместимы с его результатами, за исключением следующих главных различий. 1. Он ограничивает себя анализом одного-единственного капиталовложения, тогда как я рассматриваю всю временную структуру инвестиций - потребления. 2. Он приходит к выводу о приемлемости правила сегодняшней ценности, дисконтируемой на основе единственной процентной ставки. Я пытался явно проанализировать, что происходит, когда имеет место разница между ставками кредитования и заимствования или когда эти ставки представляют собой функцию объема займов. На основе собственных исследований я пришел к заключению об универсальной приемлемости правила сегодняшней ценности. Из этих двух различий первое действительно является очень важным. Суть изысканий Фишера заключалась именно в том, что инвестиции нельзя рассматривать изолированно, но лишь с учетом других доступных инвестиционных и потребительских альтернатив. Тем не менее в своей статье Самуэльсон удовлетворяется лишь опровержением множества заблуждений, пока еще существующих в данной области экономической теории.





