 |
Многое в теории конкурентной экономики базируется, однако, на более решающем и жестком условии, чем ограниченность, а именно на предположении о выпуклости. Производственное множество выпукло, если отрезок, соединяющий любые две точки а и b множества, содержит лишь точки, принадлежащие производственному множеству. Или, говоря неформально, множество не содержит ни дыр, ни зубцов на своих границах. Основное преимущество постулатов выпуклости состоит в том, что они, по словам Купманса, "представляют в некотором смысле минимальные допущения, гарантирующие существование системы цен, которая допускает или способствует децентрализованному принятию эффективных и согласованных решений" [57]. Никаких допущений о дифференцируемости не требуется. Максимум на выпуклом производственном множестве - не просто наибольшее значение в малой окрестности; это максимум по всему диапазону возможных производственных планов, отображенных в модели.
Представление технологических возможностей в виде множества является наиболее всесторонним подходом к анализу производства. Но для большинства практических и ряда теоретических приложений этот подход обладает слишком большой общностью, чтобы принести пользу. Множество должно быть ограничено и специализировано. Одним из таких специализированных понятий является производственная функция.
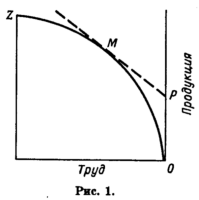
Традиционный подход к теории фирмы состоял в том, чтобы указать производственную функцию, которая описывала бы максимально достижимый выпуск продукции при данных затратах ресурсов на существующем уровне технологических знаний. В терминах рис. 1 производственная функция описывает подмножество точек, лежащих на границе OMZ. Для фирмы, выпускающей разные товары, производственная функция описывает максимальное значение выпуска одного вида продукции как функцию затрат ресурсов при условии, что выпуск всех остальных видов поддерживается постоянным. Ради упрощения анализа будем считать функцию непрерывной и дифференцируемой, причем как ресурсы, так и продукция обладают бесконечной делимостью. Тогда, если этот технологический процесс можно повторить, увеличение расхода всех ресурсов в определенное число раз должно привести к такому же пропорциональному увеличению выпуска. Короче говоря, упрощенная производственная функция принимается однородной функцией первой степени [89].
Традиционная производственная функция описывает лишь эффективные технические способы, т.е. такие, когда производится максимум желаемого товара при данных затратах ресурсов. Процесс нахождения таких технических способов не рассматривается. Долгие годы эти вопросы считались задачами управления, выходящими за рамки экономики. Но в последнее время стало ясно, что задачи размещения ресурсов внутри фирмы совершенно аналогичны задачам размещения ресурсов между фирмами и отраслями. Если перенести центр внимания снова на фирму с целью изучения ее внутренних решений, то можно не только получить экономию, но и приобрести углубленное понимание предмета.
Технологические условия наиболее полно исследованы на практике с помощью линейного анализа деятельности (activity analysis) [28]. .Производственное множество значительно упрощается. Во-первых, отметим, что существует конечное число однородных товаров "и также конечное число базисных технологических способов. Каждый базисный способ характеризуется некоторым числом для каждого товара - отрицательной величиной для затрат ресурса и положительной для выхода продукции. Технические знания общества вложены в эти базисные способы, и в применении они считаются постоянными и воспроизводимыми. Способы полагаются аддитивными. Это означает, что они независимы друг от друга; один способ можно сложить с другим и образовать новый способ, состоящий просто из суммы величин исходных способов. Каждый способ независим от других; или, другими словами, между ними нет взаимодействия. Способы считаются бесконечно делимыми и пропорционально воспроизводимыми. Так, если базисный способ выражается формулой "2 человеко-дня + 2.5 лопато-дня = 1 яма", тогда формула "2 λ человеко-дней + 2.5 λ лопато-дней = λ ям", где λ - любое неотрицательное число, также выражает возможный способ. Число λ обычно называется интенсивностью использования способа [57].
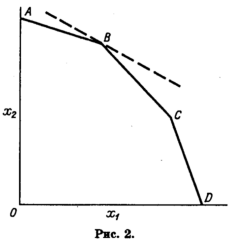 |
До сих пор мы не накладывали никаких ограничений на линейную модель анализа деятельности; множество, которое до этого момента было открытым, замыкается постулированием ограниченности ресурсов. Ресурсы можно использовать в любых неотрицательных количествах до заданного верхнего предела. Это обстоятельство ограничивает производственное множество теми точками, которые соответствуют интенсивностям способов в пределах, допускаемых этими ограничениями.1 Если дано количество всех ресурсов, можно изобразить результирующее множество в виде диаграммы для двух продуктов x1 и х2 с тремя действующими ограничениями на расход ресурсов (рис. 2). В точках В и С действуют по два ограничения, а третий из ресурсов используется не полностью.
В точках на отрезках АВ, ВС и CD действует только по одному ограничению, остальные два еще имеют резерв для использования. Новые точки, лежащие на границе ABCD, очевидно, в некотором смысле более эффективны, чем внутренние точки. Таким образом, можно формально определить набор способов как эффективный, если не существует никакого другого возможного набора способов, при котором одного вида товара производилось бы больше, а всех остальных - не меньше. (Это, безусловно, соответствует понятию эффективности, которое используется в традиционном подходе к производственной функции). Если продуктам х1 и x2, мы присвоим определенные цены, скажем р1 и р2 (которые мы считаем строго положительными), тогда максимизация функции π = р1х1 + р2х2 неизбежно приводит к выбору эффективной точки; поэтому прерывистая линия на рис. 2 проходит через точку В. Изменяя подходящим образом цены p1 и р2, но сохраняя их строго положительными, мы можем побудить предпринимателя пройти через все точки эффективного подмножества. И наоборот, каждой эффективной точке соответствует система цен, которая заставит предпринимателя, желающего максимизировать прибыль, выбрать именно эту точку [29].
Результат анализа деятельности отличается от результата анализа классической производственной функции тем, что кривая трансформации на рис. 2 состоит из ряда линейных отрезков, а не является гладкой кривой. Следовательно, предельная норма замены по мере изменения состава продукции изменяется не гладко, а "скачками" от одного значения наклона отрезка до соседнего.2 Когда базисных процессов очень много, многоугольник трансформации на рис. 2 будет состоять из множества отрезков, поэтому модель анализа деятельности будет приближаться к классической производственной функции.
И в том и в другом представлении технологических возможностей мы полагали процесс производства, или деятельность, постоянным и воспроизводимым при сходных условиях. Если нет ограничений на количество ресурсов, это означает, что каждая фирма в силу постулатов обладает одним и тем же производственным множеством. Согласно постулату пропорциональности, каждая фирма имеет постоянную отдачу от масштаба. В условиях совершенной конкуренции каждая фирма будет получать нулевые прибыли, какими бы ни были масштабы ее операций. Таким образом, эта модель оставляет неопределенным долгосрочный равновесный уровень объема производства фирмы. Такой результат, очевидно, не может нас полностью удовлетворить, и мы как-то должны объяснить существование фирм и их распределение по размеру.
Неоклассический метод разрешения этой проблемы был предложен Калдором [54]. Предположим, что мы определили для каждой фирмы существенный элемент, называемый "предпринимательством". Его нельзя купить на рынке, это специфическое личное качество каждого члена коллектива. Фирма существует, когда каждый ее сотрудник применяет свои предпринимательские способности. Но поскольку предпринимательские способности зависят от личности, то и производственная функция будет меняться от одного человека к другому. Эта гипотеза "объясняет" как существование фирм, так и распределение их по размеру. Такое объяснение недостаточно, но, пока не придумано лучшего, придется довольствоваться им.
Вследствие того что модель анализа деятельности предприятия основана на технологических процессах фирмы, введение предпринимательских способностей в эту модель встречает немало трудностей. Ясно, что наилучшим подходом было бы рассмотрение количества предпринимательства как характеристики различия ограничений объема предпринимательства в длительном. периоде. Но это невозможно, поскольку не существует общепринятой количественной меры предпринимательства.3 Следует сделать общий вывод, что подход, основанный на анализе деятельности, не может решить задачу долгосрочного распределения продукции между фирмами. К счастью, решение этой проблемы не является главным и даже важным для основы экономической теории.
Современные разработки теории роста содержат немало специальных гипотез о производственных функциях. Одно полезное различие, тесно связанное с функциями периода классического анализа, которое проводится в ряде работ [47, 84], касается различия между производственными функциями ex post и ex ante.
Функция ex ante содержит полный набор возможностей замещения, открытых для предпринимателя, когда он выбирает свой способ производства. Функция ex post показывает возможности, доступные после того, как способ производства выбран. Этому различию можно придать форму специальной математической функции, используемой для описания соотношений.
2. Производственные функции и агрегирование
Существует широкий выбор алгебраических выражений, которые можно использовать для представления производственных функций. Простейшая модель - это специальный случай общей модели анализа производства. Если фирме доступен только один вид деятельности, то производственную функцию можно представить прямоугольными изоквантами с постоянной отдачей от масштаба. Возможность изменять соотношение факторов производства отсутствует, и эластичность замены, безусловно, равна нулю. Это крайне специализированная производственная функция, но ее простота объясняет ее широкое применение во многих моделях.
Вероятно, наиболее популярна производственная функция Кобба-Дугласа [21]. В своей наиболее известной форме, когда Х означает объем производства, К - размер капитала и L - затраты труда, она записывается в виде
X=ALαKβ,
Х > 0, α≥О;
К > О, β≥ 0;
L > О, A > 0.
Свойства функции Кобба-Дугласа следующие.
а) α и β - показатели эластичности производства по отношению к труду и капиталу соответственно.
б) Степень однородности функции равна α + β. Если α + β превышает единицу, налицо возрастающая отдача от масштаба;α + β = 1 указывает на постоянную отдачу.
в) Предельная физическая продуктивность труда, например, при α < 1, изменяется обратно вложенному труду, т.е. уменьшается при увеличении последнего. Соответственно вторая производная ∂2X/∂L2 = α(α - 1)X/L2 отрицательна при α < 1.
г) Предельная норма замещения равна αK/ βL, поэтому эластичность замещения равна единице.
Из производственной функции Кобба-Дугласа и цен продукции (Р), труда (W) и капитала (I) можно вывести функцию затрат и уравнение предложения для условий конкурентного рынка. После подстановки выражений для предельной производительности в уравнения производства получим функцию затрат в виде
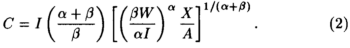
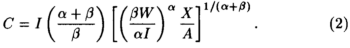
Подобным образом функция предложения может быть получена приравниванием ∂С/∂Х к Р, что после преобразований дает
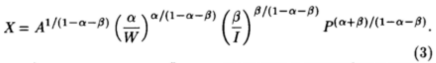
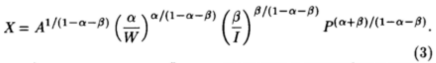
Функция затрат линейна по отношению к логарифмам ставки заработной платы, цены капитала и объема продукции. Если α + β = 1, затраты пропорциональны выпуску продукции и кривая предложения обладает бесконечной эластичностью. Можно было бы опустить предположение о конкурентности и ввести эластичности предложения факторов производства, чтобы получить неконкурентные функции затрат, но вычисления становятся утомительными.
Функция Кобба-Дугласа имела долгую и успешную жизнь без серьезных соперников, но недавно ей составила сильную конкуренцию новая функция Эрроу, Ченери, Минхаса и Солоу [5, 6], которую мы будем называть сокращенно SMAC.4 (Браун и Де Кани также разработали эту функцию независимо [13]). Основное отличие функции SMAC заключается в том, что вводится постоянная эластичности замещения σ, отличная от единицы (как в функции Кобба-Дугласа) и нуля (как в модели затраты- выпуск). Функция имеет вид
X = γ [δ K -ρ + (1-δ) L -ρ)] -1/ρ (4)
Это однородная функция первой степени, так что отдача от масштаба постоянна. Параметр эффективности γ определяет объем продукции при данных затратах ресурсов; параметр распределения δ (0 < δ < 1) отвечает за деление фактора дохода. Параметр замещения (р) является простой функцией эластичности замещения, поэтому σ = 1/(1 + ρ). Предельный продукт капитала равен δγ (-ρ)(X/K)(1+ρ). Пределы для величины ρ выводятся из σ. Когда эластичность бесконечна, ρ = 1; а когда эластичность равна нулю, ρ = ∞.
За счет подбора подходящих значений σ функцию SMAC можно привести как к форме затраты-выпуск, так и к форме Кобба-Дугласа. Когда σ стремится к единице (т.е. ρ → 0 ), функция SMAC переходит в функцию Кобба-Дугласа. Продемонстрируем это следующим образом:
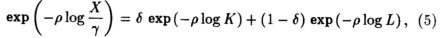
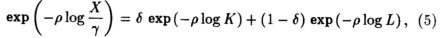
и, следовательно,
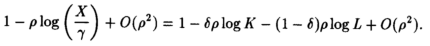
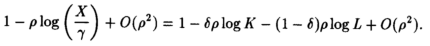
Деля на ρ, при ρ → 0, в пределе получим
Х = γK δ L 1-δ. (6)
Это функция Кобба-Дугласа с постоянной отдачей от масштаба.
Аналогичным образом можно показать, что предельная форма при ρ → ∞ представляется рядом прямоугольных изоквант с расположением углов на луче, исходящем из начала координат. Вместо преобразования функции SMAC ее можно обобщить, чтобы учесть случаи возрастания и убывания отдачи от масштаба путем введения еще одного параметра ν:
X = γ[ δ K-ρ + (1 - δ)L-ρ] -ν/ρ, ν>0. (7)
Если ν > 1, налицо возрастание отдачи от масштаба, а если ν < 1, отдача уменьшается [71].
Функции затрат и предложения можно вывести из функции SMAC (при ν = 1) путем подходящих подстановок. В случае совершенной рыночной конкуренции получаем кривую затрат длительного периода (капитал считается независимой переменной):
С = KZ, (8)
где
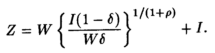
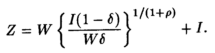
Используя соотношение между капиталом и объемом продукции, получаем функцию затрат длительного периода с объемом продукции как независимой переменной:
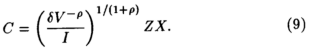
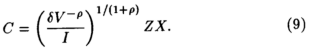
Затраты являются линейной функцией объема продукции, как и следовало ожидать, от однородной функции первой степени. Соотношение между затратами и ценами факторов, конечно, более сложное, чем в случае Кобба-Дугласа.
Выбор той или иной модели производственных соотношений зависит от многих условий. Важным критерием следует считать тот вес, который модель придает разумно агрегированным соотношениям, которые в некотором смысле соответствуют микросоотношениям.
Производственная функция - это технологическое соотношение, стоящее перед фирмой. Именно предприниматель выбирает нужные пропорции и уровни объема продукции. Можно ли перейти к построению полезных производственных функций для отрасли или для промышленного или сельскохозяйственного сектора в целом? Сразу видна одна трудность: те факторы, которые мы считали фиксированными для отдельной фирмы, вовсе не обязательно будут фиксированными для отрасли, например предпринимательская способность. Другие факторы, такие как количество квалифицированного труда, которые не были фиксированы для отдельной фирмы, вполне могут быть значительно ограничены для отрасли.5 Даже если бы у всех фирм была растущая отдача от масштаба, это еще не означало бы, что отрасль в целом также получает экономию от масштаба. Расширение отрасли часто сталкивается с менее удобными местами, ограниченным предложением сырья и т.д. При обсуждении задачи агрегирования удобно было бы отвлечься от трудностей, связанных с положительными и отрицательными внешними эффектами.6 В частности, мы будем полагать производственные функции отдельных предприятий не зависящими от совокупного производства отрасли.
Систематическое исследование общей задачи агрегирования производственных функций было развито в пионерской статье Клейна [55]. Для получения агрегированной (строго говоря, усредненной) производственной функции и агрегированных отношений предельных продуктивностей, аналогичных микрофункциям, он предложил построить взвешенное геометрическое среднее из соответствующих микропеременных, где веса были бы пропорциональны эластичностям для отдельных фирм. Эластичности макрофункции представляют собой взвешенное среднее микроэластичностей, причем веса пропорциональны затратам на факторы. Макровыручка представляется произведением макроцены на макроколичество, которое определяется как арифметическое среднее микровыручек; аналогичным образом определяются макроставка заработной платы и макрозатраты капитала.
Клейновское агрегирование по фирмам имеет ряд любопытных следствий. К примеру, определение макроставки заработной платы W таково:
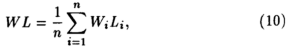
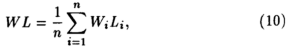
где Wi и Li - ставка заработной платы и (однородный) труд, вложенный на i-й фирме, а


есть определение вложенного макротруда, в котором αi, представляет собой эластичность труда на i-й фирме. В условиях конкуренции на всех фирмах одна и та же ставка заработной платы W* = Wi для всех i. Поэтому после подстановки получим
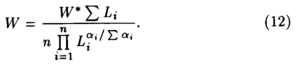
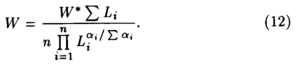
Таким образом, макроставка заработной платы будет почти всегда отличаться от общей ставки фирм. В этом простом случае трудно интерпретировать W и понять, почему она должна отличаться от W*.7 Подобные же замечания можно сделать относительно цен продукции и капитала.
Большой вклад в формальную теорию агрегирования внес Натаф [73]. Он доказал, что при разумном агрегировании производственная функция должна быть сепарабельной. При этом объем продукции равен сумме двух составляющих, одна из которых связана с трудом, а другая с капиталом.8 Это условие накладывает сильные ограничения. Из трех уже рассмотренных производственных функций модель затраты-выпуск, очевидно, сепарабельна. Функция Кобба-Дугласа не отвечает этому условию, но после логарифмического преобразования становится сепарабельной; это объяснение клейновского использования средних геометрических.9 Конечно, функция Кобба-Дугласа хорошо подходит для агрегирования, особенно на уровне фирмы.10 Указанным свойством обладает и производственная функция SMAC. Ее можно записать в виде
γ ρX -ρ = δ L -ρ + (1 - δ) K -ρ. (13)
Это сепарабельная функция, удовлетворяющая условиям Натафа.
Одна из основных практических проблем агрегирования заключается в том, что данные обычно публикуются в виде арифметических средних или итогов, тогда как наша система агрегирования требует геометрических средних. Каковы ошибки, возникающие при такой аппроксимации? Можно показать, что, если отклонения от среднего значения относительно малы, среднее геометрическое (G) приближенно связано со средним арифметическим формулой
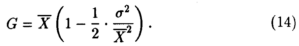
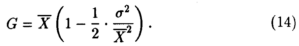
В этом случае арифметическая величина дает относительное смещение вверх приблизительно на половину относительной дисперсии. Отсюда следует, что если относительные дисперсии переменных - продукции, капитала и труда - приблизительно равны, то относительные смещения будут близки. Это верно, впрочем, лишь при условии относительно малых отклонений от средних значений, а данное условие на практике часто не выполняется.
Статистические задачи линейного агрегирования рассматривались Тейлом [92]. Тейл исследует, насколько законно применение макроотношений к агрегированным уровням при заданных микроотношениях и виде агрегирования. Рассмотрим производственную функцию Кобба-Дугласа в логарифмической форме для i-й фирмы:
xi = αili + βiki +аi, i=1,...,n, (15)
где xi = log Xi , li = log Li и ki = log Ki.
Отсюда будем искать производственную макрофункцию
x = αl+ βk + a + ε
для наблюдаемых агрегированных уровней временного ряда. Сначала рассмотрим регрессию затрат труда на i-й фирме по случайным агрегированным затратам труда и капитала для наблюдений, представленных временным рядом, т. е.
li = Bli l + Cli k + Dli + Uli, (17)
Подобным же образом вычисляется регрессия капитала:
ki = Bki l + Cki k + Dki + Uki. (18)
Коэффициенты регрессии В иСописывают систематические движения микропеременных как макровеличинное изменение. Случайные переменные U обладают обычными характеристиками. Подставляя эти уравнения в микроуравнение (15), получим
х = αl + βk + а, (19),
где
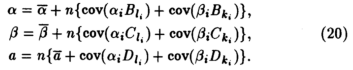
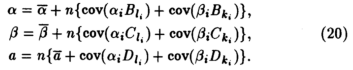
Смещение оценок макропараметров при агрегировании измеряется ковариационными членами уравнений. К сожалению, трудно развить эти результаты дальше, поскольку нелегко предложить априорные ограничения на величину ковариаций. Количественной величине смещения еще предстоит статистическая оценка.
После обзора проблем агрегирования нетрудно усомниться вообще в применимости такого понятия, как агрегированная производственная функция. Разнообразие рыночных и технологических условий, какое наблюдается в современной экономике, внушает мысль о невозможности удовлетворить основным требованиям разумного агрегирования, за исключением, может быть, отдельных фирм в одной и той же отрасли или ограниченных секторов экономики.
3. Технологические и производственные функции, основанные на инженерных расчетах
Развитие экономической теории на основе сведений о технологических процессах дало повод к разработке производственных функций и функций затрат с использованием технических достижений инженерной и сельскохозяйственной науки. Эта научная информация получена либо экспериментально, либо из повседневной инженерной практики. Подход к производственной функции на технической основе обладает значительными преимуществами, поскольку, во-первых, известна область применимости функции, а во-вторых, он позволяет относительно легко включить результаты технического прогресса. Более того, в отличие от подхода, основанного на статистическом анализе множества объектов и временных рядов, мы не связаны жесткими рамками фактических наблюдений.
Основной предмет изучения, инженерный "процесс", определяется так, как это удобно с точки зрения инженерного анализа. Подобным же образом объемы ресурсов часто указываются в технических единицах, например в единицах теплоты. Первой задачей является перевод технических единиц в величины, более подходящие для экономического анализа. Для этого может потребоваться описание других процессов, например производства тепла путем приобретения и сжигания топлива. Вторая и наиболее важная задача заключается в том, чтобы путем объединения этих процессов на отдельном предприятии получить производственную функцию предприятия. При определении и исследовании технологических функций следует стремиться к тому, чтобы функции были независимыми и аддитивными. К счастью, инженер тоже стремится избежать эффектов взаимодействия при описании процессов, которыми он занимается, так что подходящее агрегирование процессов на предприятии часто достигается с приемлемой точностью.
Технологическая функция и производственная функция предприятия, полученные на инженерно-технической основе, отличаются от традиционной производственной функции экономической теории. Во-первых, фактор предпринимательства не включается явно в технологическую функцию. Технические данные могут отражать наиболее эффективный управляемый процесс или "среднестатистический" уровень промышленности. Предпринимательство тогда входит в технические данные непосредственно. Во-вторых, технические данные могут описывать только технические процессы. Нелегко описать техническим языком, например, нетехнический процесс продажи товаров. А это означает, что функции, выведенные таким образом, не отражают всех видов деятельности предприятий; поэтому их следует называть технологическими функциями, или функциями предприятия, в отличие от более широкого понятия производственной функции фирмы.
Такой метод составления производственных функций широко использовался в сельском хозяйстве. Хеди и его коллеги [42] вывели свои функции экспериментально; например
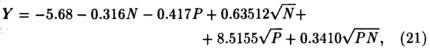
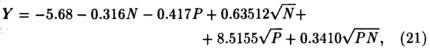
где Y - урожайность зерна в бушелях на акр; N - число фунтов азота; Р - число фунтов фосфата. По этому выражению можно рассчитать предельную продуктивность каждого удобрения, а затем найти оптимальную комбинацию удобрений для различных уровней относительных цен. Но, конечно же, функция не говорит нам, сколько требуется земли или менеджеров. Следовательно, это строго технологическая функция.
Ченери и Фергюсон [16, 36] первыми стали использовать Технические данные в промышленных технологических функциях. В своем исследовании перекачки природного газа Ченери использовал инженерно-технические принципы газового производства для получения технологической и производственной функции для газопровода; результат показал возрастание отдачи от масштаба. Фергюсон изучал технологию коммерческих воздушных перевозок с целью вывести производственное соотношение. Он занимался измерением агрегированной технологической функции, но включил в нее только прямые затраты ресурсов; расходы на администрацию, к примеру, он не учитывал. (Он также описал ход технического прогресса в 1939-1947 гг.). Технология химической промышленности изучалась Муром [70], причем было показано общее возрастание отдачи от масштаба. Вообще это, кажется, является общим результатом большей части инженерно-технических работ.11
Технологические функции и производственные функции предприятия пригодны для целого ряда различных целей, например для вывода кривых затрат предприятия, прогнозирования потребности в сырье и рабочей силе и т. д. Однако эти функции непригодны для проверки гипотез об экономии от масштаба фирмы. Даже если технологическая функция, или функция предприятия, показывает возрастающую отдачу, это еще не значит, что фирма фактически получает такие доходы. Рост доходов за счет технологических процессов может быть съеден высокими административными затратами и др.
Технологические функции особенно полезны при анализе технического прогресса. Хирш [43, 44] показал, как улучшение технологических процессов дало уменьшение затрат труда при увеличении выпуска продукции. Эта технологическая функция в инструментальной промышленности предполагала, что удвоение совокупного продукта дало уменьшение затрат труда на 18-20% [7].12
Развитие технологических функций на основе инженерно-технических данных с помощью моделей линейного программирования стало наиболее значительным достижением экономики фирмы в последние годы [63, 64]. Технологические возможности фирмы представляются конечным набором способов, а технические ограничения вводятся в виде фиксированных объемов некоторых ресурсов, таких, к примеру, как ограниченная производственная площадь. Используя симплексный или другой вычислительный метод, экономист может определить оптимальную комбинацию способов для любой заданной системы цен.
При сравнении подхода на основе линейного программирования с эмпирическим исследованием традиционных производственных функций следует иметь в виду следующее. Во-первых, модель линейного программирования обычно интерпретируется как модель производства в коротком периоде с фиксированным предложением ряда ресурсов. С другой стороны, эмпирическое исследование производственных функций Кобба-Дугласа обычно связано с долгосрочными соотношениями, в которых все ресурсы переменные. Во-вторых, решение задачи с помощью модели программирования указывает, что фирмы должны делать, чтобы максимизировать свой чистый доход; в некотором смысле это улучшает существующую производственную функцию фирмы, придавая ей более высокий уровень эффективности. Подход на основе линейного программирования не просто описывает производственные отношения, обычно он меняет их!
Применение, инженерно-технических данных для расчета производственных функций еще переживает период младенчества. Однако вот уже много лет такая информация используется при анализе затрат, особенно бухгалтерами, а в последнее время и экономистами. Эти методы и результаты освещаются в разделе 7.
4. Статистические модели:
идентификация и оценка
идентификация и оценка
Формальное описание модели производства может иметь широкий спектр - от одного простого уравнения до "полной системы" уравнений. Однако все модели независимо от того, используют ли они агрегированные или микроданные, относятся ли они к множеству объектов или к временным рядам, затрагивают одни и те же проблемы описания и интерпретации; к ним-то мы сейчас и обратимся.
Вероятностные аспекты моделей производственных функций типа одновременных уравнений в явном виде впервые были введены в важной статье Маршака и Эндрюса [65]. Они писали, что "производственная функция (1) будет меняться даже в одной отрасли промышленности, от предприятия к предприятию и от года к году в зависимости от технических знаний, воли, усилий и удачи данного предпринимателя - эти факторы можно объединить в понятии "техническая эффективность" и представить одним или несколькими случайными параметрами". Они выдвинули простую гипотезу:
Y0 = A0Y1α1 Y2α2 U2, (22)
где Y0, Y1 и Y2 - соответственно объем продукции, труд и капитал; U0 - случайная переменная, среднее значение которой равно единице. (Это новое обозначение с нижними индексами будем использовать в дальнейших рассуждениях). Маршак и Эндрюс интерпретируют возмущение как аналог экспериментальной ошибки, но на самом деле оно имеет более широкий смысл. Колебания выпуска продукции на отдельной фирме от года к году могут быть обусловлены экзогенными случайными причинами (такими, как погода), но разница между одной фирмой и другой из-за различной "способности" предпринимателя останется постоянной в течение длительного периода [72, 74]. Совершенно иная интерпретация возмущений требуется в случаях анализа на множестве фирм и анализа временных рядов.
Отношение предельной производительности также в среднем не будет выполняться с достаточной точностью, отклонения же можно описать случайной переменной. Пусть реальная заработная плата составляет Р1/Р0, где Р1 - денежная ставка заработной платы, P0 - цена продукции; тогда
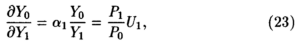
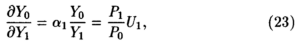
где U1 - случайный член, среднее значение которого равно единице. Маршак и Эндрюс утверждают, что "не у всех предпринимателей хватит настойчивости, способностей и просто везения, чтобы выбрать наиболее выгодную комбинацию производственных факторов - если у предпринимателя А техническая эффективность такая же, как и у В, то "экономическая эффективность" может быть и ниже".
И в этом случае нужно внимательно отнестись к интерпретации роли возмущений. Во-первых, рассмотрим интерпретацию U1 при анализе на множестве объектов. Возмущение можно понимать как свойство отдельного предпринимателя - отражение его "способности".13 Но можно ли описывать вариации "экономической эффективности" от одного предпринимателя к другому случайной переменной? Безусловно, в какой-то фиксированный момент времени это допустимо. Но более точно, чем константа, отразят способность предпринимателя несколько значений показателей фирмы, взятых через некоторый промежуток времени. У эффективно действующего предпринимателя среднее значение U1 будет близко к единице и дисперсия по времени невелика, а у неэффективно действующего среднее значение U1 будет сильно отличаться от единицы и дисперсия, вероятно, будет иметь большое значение.14 Приведенное описание взаимосвязей между величинами U, конечно, очень важно, но на самом деле об этих возмущениях известно довольно мало...
7. Функции затрат
Вместо оценки производственной функции мы можем непосредственно оценить функцию затрат. Ее можно вывести из приведенной формы соотношений продукции и предельной производительности. На практике анализ кривых затрат часто намного более удобен, чем оценка производственных функций, так как имеющиеся данные о затратах обычно приводятся в денежном выражении.
Было предпринято много попыток установить форму кривых затрат с помощью теоретических выкладок. В частности, считалось, что вид функции затрат для короткого периода очевиден из принципа уменьшающейся отдачи; и этот закон или принимался в качестве аксиомы, или доказывался с помощью аргументов типа reductio ad absurdum. Однако Менгер показал: предположение об уменьшающейся предельной отдаче совсем необязательно вытекает из предположения, что производственная функция является: а) ограниченной и б) неубывающей. Из твердого предположения, что производственная функция является субоднородной и возрастающей по отношению к одному фактору, необязательно должен следовать закон убывания предельного продукта; твердо мы можем вывести только закон убывания среднего продукта. Однако большинство экономистов до сих пор рассматривают уменьшающуюся предельную отдачу в качестве более чем обещающей гипотезы.
Существует еще одна гипотеза о том, что предельные затраты короткого периода постоянны в широких диапазонах выпускаемой продукции. Эта теория поддерживается исследователями, которые интенсивно изучали производственную деятельность предприятий [З]. Она также служит основной предпосылкой в работе бухгалтеров, и, таким образом, практически она оказывается самой популярной гипотезой. Никто не предпринимал попыток показать, что эта форма функции затрат короткого периода является обязательным следствием некоторого набора фундаментальных и самоочевидных постулатов. Те, кто поддерживали эту гипотезу, спорили только о том, является ли это их функцией затрат [31], по мнению бизнесменов, или что эта гипотеза единственная, удовлетворяющая эмпирическим наблюдениям [53].
Традиционная теория фирмы не слишком-то помогает в создании кривой функции затрат длительного периода, как это было для короткого периода. Все согласны, что с данными ценами факторов долгосрочные средние затраты убывают при низких уровнях выпуска продукции. Прежде всего экономия от масштаба возникает от простоты обращения с большими количествами. Второй причиной считается распределение риска и уменьшение затрат, связанных с неопределенностью [96]. Третьей и, вероятно, наиболее общепринятой причиной падения затрат является неделимость людей и оборудования. Крупное оборудование обычно более производительно, чем мелкое. Для каждого технологического процесса оптимальный размер оборудования может меняться, поэтому для уменьшения средних затрат до минимума требуются высокие параметры оборудования. Естественно, что вначале средние затраты будут уменьшаться с увеличением размера, но пока почти не достигнуто согласие о форме кривой при дальнейшем увеличении выпуска продукции. Е. А. Дж. Робинсон доказывал, что координация управления и контроля становится все менее эффективной, поэтому возрастающие затраты на управление приводят к росту средних затрат длительного периода. Саржан Флоренс и другие критикуют такое объяснение на основании того, что эти предположения не были проверены ни в одном систематическом эмпирическом исследовании. Можно также спорить о том, что последние достижения в развитии вычислительной и другой управленческой техники привели к повышению относительной эффективности больших управленческих органов.
Подводя итоги, можно сказать, что теоретические доводы позволяют предположить: кривая краткосрочных средних затрат имеет типичную U-образную форму, хотя Менгер высказал некоторые сомнения. Теория вполне очевидна в отношении допущения, что можно в начале ожидать предполагаемое уменьшение долгосрочных средних затрат при увеличении масштаба производства. Но для высокого уровня выпуска теоретические доводы не кажутся столь убедительными.15 Выбор между альтернативами должен зависеть от эмпирических данных.
Экономическая теория определяет затраты для фирмы как те выплаты, которые необходимо произвести, чтобы заставить факторы производства продолжать действовать вместе с фирмой. Выплаты владельцам производственных факторов, которые являются специфичными для конкретной фирмы и которые ничего не стоят, если они не используются этой конкретной фирмой, являются рентами или, как их называет Стиглер, расходами без стоимости (non-cost outlays). Расходы на услуги, специфичные для отрасли, являются расходами для отдельной фирмы, но расходами без стоимости, когда это касается отрасли в целом. Также удобно разделить затраты на постоянные и переменные. Постоянные затраты соответствуют любому уровню выпуска продукции, в то время как переменные возрастают или уменьшаются вместе с объемом выпускаемой продукции. Изменение затрат также зависит от периода приспособления. За короткие промежутки времени "завод" невозможно изменить. Существующее оборудование может либо использоваться, либо простаивать. За длительный период времени можно изменить все факторы производства, за исключением тех, которые являются специфичными и постоянными для конкретной фирмы, такие как предпринимательские способности.
Определение затрат, принятое теоретиками, естественно порождает серьезные трудности при его использовании. Сначала обратимся к концепции длительного периода. Рассматриваемые альтернативы включают изменение всех факторов, за исключением тех, которые являются постоянными для конкретной фирмы. Все выплачиваемые фирмой суммы, кроме отдачи на постоянные вложения, специфичные для фирмы, следует рассматривать как затраты. Соответствующее определение затрат таково, что суммарный годовой доход меньше, чем доход от предпринимательских способностей. Но, конечно, не существует никакой эмпирической меры для отдачи от предпринимательства. Однако из этого тупика есть выход. Мы предположили, что предпринимательский долгосрочный выбор заключается в том, чтобы либо ничего не производить, либо производить какое-то количество конкретного продукта своей отрасли. Но очевидно, что предприниматель может также перевести свои предпринимательские способности в другие отрасли. Если его ожидаемый предпринимательский доход в другой, "наиболее подходящей" отрасли будет лишь немного ниже его ожидаемого дохода в его теперешней отрасли, то тогда это можно рассматривать как затраты производства. Следовательно, подходящим эмпирическим определением являются суммарные выплаты, которые идентичны суммарному годовому доходу. Тогда средние долгосрочные затраты равны цене [39]. Данные о ценах обычно имеются, и некоторые очень стремятся использовать модель совершенной конкуренции везде, где это кажется возможным [18].
Для отрасли или для фирмы в явно монополистической ситуации "ценовое" определение долгосрочных средних затрат обычно неприемлемо. Цена включает в себя элементы монополистической прибыли на единицу выпускаемой продукции. Очевидно, что специфические факторы, контролируемые фирмой, которые не могут быть проданы, являются производными от ренты и соответствующие расходы должны быть исключены из затрат. Эти "факторы" могут включать весьма специфический навык предпринимателя, который является еще и природным даром, эксклюзивные местные права монополии, предоставленные государством, лицензии на общественную деятельность, членство в Королевской хирургической коллегии и т.д. Ни один из этих атрибутов нельзя купить на рынке. Остаточный доход от подобных факторов является чистой рентой. Основная трудность заключается в получении статистических данных для оценки этих затрат без стоимости. На практике приходится пользоваться данными бухгалтерских отчетов. Большинство исследователей исключили из затрат бухгалтерскую прибыль. Вероятно, в большинстве случаев из-за этого получается недооценка затрат. Но никто не знает, влияет ли такое смещение на форму эмпирических кривых затрат. Чтобы судить об этом, необходимо тщательное изучение бухгалтерской отчетности.
При изучении коротких периодов появляются некоторые факторы, типичные затраты капитала, которые привносят увеличение постоянных затрат для отдельных фирм. Их доходы являются квазирентами и не должны рассматриваться как затраты в коротком периоде. Должны учитываться только краткосрочные переменные затраты. Трудно подобрать эмпирическое соотносительное понятие для этих затрат. В принципе мы должны либо измерять квазиренты таким же образом, как и ренты, либо непосредственно идентифицировать и оценивать краткосрочные переменные затраты. На практике исследователи часто использовали понятие "прямые затраты", которое исключает "накладные затраты" [27]. Но обычно это не годится, потому что оно не включает многие затраты (например, затраты труда в главном управлении, которые являются переменными), а также, вероятно, включает некоторые затраты (например, часть расходов на некоторое оборудование), которые не являются переменными.16 Другая общепринятая процедура заключается в использовании суммарных бухгалтерских затрат. Бухгалтерские положения меняются, и трудно сказать, будут ли суммарные краткосрочные переменные затраты недооцениваться или переоцениваться. Но можно легко убедиться, что изменения в бухгалтерских затратах тесно коррелированы с изменениями истинных затрат. Например, можно предполагать, что изменения в квазирентах отразятся на бухгалтерских доходах, но не на бухгалтерских затратах. На основании этого можно предполагать, что с помощью бухгалтерских данных можно четко оценивать предельные затраты. Однако надо немного подробнее рассмотреть недостатки в бухгалтерской практике.
Положения, принятые бухгалтерскими службами, неодинаковы в разных странах; но в широком смысле для большинства бухгалтерских данных характерны следующие недостатки.
а) Единичный период для бухгалтерских целей отличается от единичного экономического периода. Вообще финансовый год длиннее, чем краткосрочный период традиционной теории.
б) Распределение амортизации активов за время их существования обычно определяется налоговыми органами, а не экономическими критериями. Типичные законы налогообложения требуют, чтобы фирма пользовалась методом "линейной" амортизации, если даже она имеет такую же протяженность существования, как и оптимальная, не принимая во внимание "затраты пользователя".
в) Оценка услуг капитала скорее относится к исторической стоимости, чем к текущим ценам.
г) Оценка запасов часто основана на некоторой общепринятой методике (например, в Великобритании "по затратам или по их текущей оценке, что из них ниже").
Эти недостатки не являются слишком серьезными для оценки функции затрат; с некоторыми неточностями можно справиться с помощью подходящей обработки [52]. Бухгалтерские данные для фирм с разнообразной выпускаемой продукцией ставят множество проблем. Они порождают желание использовать бухгалтерские методы для распределения накладных и комплексных расходов и затрат. Но из-за произвольных методов, используемых в бухгалтерском учете и распределении, большинство аналитиков отказываются от этого решения. Тем не менее с помощью данных учета затрат можно сделать многое.
Инженерные данные редко использовались экономистами для оценки функций затрат. Результаты инженерных исследований не так уж часто сформулированы в таком виде, чтобы их было легко перевести на язык экономики. Первые систематические попытки решения этой проблемы экономистами были предприняты Ченери и Фергюсоном [16, 35]. Ченери предложил описывать производственные функции и функции затрат в терминах наблюдаемых (или проектируемых) инженерных переменных. В своем примере с передачей по трубопроводам Ченери определил затраты как функцию от диаметра трубы, вязкости, коэффициента сжатия и мощности насосов. Фергюсон исследовал "предельные топливные затраты" авиации, преобразуя инженерные производственные функции в функции затрат.17
Основные ограничения инженерных данных подобны ограничениям данных бухгалтерских затрат. Действительно, эти два набора данных часто очень тесно связаны. Бухгалтеры оценивают товарные затраты, разделяя производство на отдельные операции, и описывают затраты каждой операции, оценивая вложения труда и т.п. Инженерные данные, подобно цифрам бухгалтерских калькуляций, относятся к процессам. Одна из трудностей
перевода этих результатов в функции затрат для некоторых отраслей заключается в том, что процессы и затраты на эти процессы могут взаимодействовать друг с другом и могут не быть сепарабельными. Однако на практике это может служить вполне достаточным приближением для множества разных отраслей. Второй главной трудностью является произвольность распределения комплексных затрат. Кажется, именно это послужило причиной того, что существует очень мало синтетических или инженерных исследований затрат многопродуктовых фирм. За последние годы самым важным применением синтетического подхода экономистов к затратам стало исследование перевозок Мейером, Пеком, Стенасоном и Цвиком [68]. Они распределили совместные железнодорожные расходы между пассажирскими и грузовыми перевозками посредством синтетического анализа взаимосвязей. Затраты на эти конкретные совместные производственные услуги были представлены в виде линейной комбинации пассажирской и грузовой нагрузок. Коэффициенты, полученные из данных уравнений, были использованы для распределения общих затрат. Это исследование стало важным шагом вперед в сфере инженерных или синтетических исследований затрат.
Несмотря на все возражения, которые могут быть высказаны против синтетического подхода к затратам, во многих случаях он оказывается единственным приемлемым методом. Вероятно, он является единственным практическим подходом для фирмы, выпускающей множество разных продуктов. Для улучшения оценок можно воспользоваться экономической теорией в сочетании с новой вычислительной техникой, в частности для обеспечения наиболее приемлемого распределения общих затрат.
Одно из самых важных различий в эмпирических функциях затрат заключается в разнице между исследованиями по множеству объектов и по временным рядам. При изучении по данным временных рядов видно, что изменения спроса приводят к возникновению различных уровней равновесного объема производства. Объем продукции и число фирм в отрасли приспосабливаются к новым уровням спроса. Для конкретной фирмы временной ряд выпускаемой продукции и суммарных затрат должен в идеале показывать функцию затрат для фирмы. С другой стороны, в исследованиях на множестве фирм в конкурентной отрасли нет наблюдаемой независимой силы, такой как спрос, которая создает различные уровни равновесного объема производства. При анализе на множестве объектов цена продукции одинакова для всех фирм. Как утверждал Фридмен, если мы определим общие затраты как идентичные общим поступлениям, исследование на множестве фирм несомненно даст неизменные средние затраты [39]. Фридмен считал, что в конкурентной отрасли разные объемы выпуска в фирмах могут появиться или за счет "ошибок", или за счет существования специфических ресурсов, контролируемых фирмой. Связь таких изменений в выпуске продукции с постоянными затратами нельзя рассматривать как свидетельство в пользу существования неизменных средних затрат длительного периода.18
Критика Фридмена настолько сильно опровергает эмпирические результаты, что требуется дальнейшее изучение. Предположим, что мы пересмотрели затраты, чтобы исключить доходы, получаемые за счет факторов, специфичных для фирмы (например, за счет предпринимательских способностей), а затем вычислили регрессию этих затрат на выпуск продукции; можно ли рассматривать результаты как некоторого рода среднее из кривых долгосрочных средних затрат отдельных фирм? Действительно, кривая регрессии покажет нам, как с изменением продукции менялись предпринимательские способности. Это весьма ценный результат, но он не имеет тесной связи с кривой затрат отдельной фирмы. Конечно, подобные критические высказывания неприменимы к исследованиям фирм при монополистических условиях [52]. Но тогда самой важной становится проблема оценки затрат и активов. А если рассматривать дифференциацию продукции как причину различных объемов выпуска, тогда концепция кривой затрат становится совершенно неясной.19 Фридмен не уничтожил полностью метода анализа на множестве объектов, но нанес ему тяжелый удар.
Уравнение, определяющее зависимость суммарных затрат от объема выпуска, используемое большинством авторов, обычно квадратичное:
C(Y) = γ + γ1Y + γ2Y2 + ε, (24)
где Y - текущий объем выпуска; ε - случайное возмущение, распределение которого полагается независимым от Y. Это приводит к возрастанию функции предельных затрат, которая оказывается линейной относительно объема выпуска. Клейн [56] недавно высказал предположение, что огиву логарифмически-нормального распределения можно использовать для кривой общих затрат традиционной формы. Только Ломаке и Нерлов использовали линейную логарифмическую кривую затрат. Это весьма удивительно в свете того, что логарифмическая функция затрат выводится из системы уравнений вида Кобба-Дугласа. Если предположить, что в уравнениях предельной производительности нет ошибок, то кривую затрат можно описать следующим образом:
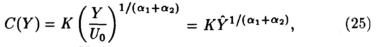
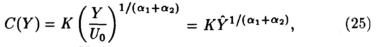
где К - постоянная; Y - выпускаемая продукция. Во временном ряде случайная переменная U0 будет отражать влияние делового цикла, погоды и т. п. При анализе на множестве объектов U0 будет измерять в основном предпринимательские способности. Затраты будут варьировать в значительной мере в соответствии с предпринимательскими способностями. Величина Y/U0 = Y^ может быть названа планируемой или средней продукцией в зависимости от того, применяется ли эта модель к временному ряду или к данным множества объектов. Вычисляя логарифмы, видим, что log U0 никогда не распределяется независимо от log Y0, поэтому достоверную оценку 1/(α1 + α2) нельзя получить с помощью стандартного метода наименьших квадратов. Но в случае коммунальных предприятий, когда продукцию можно считать экзогенной переменной, это возражение отпадает [75].
Было предпринято очень мало попыток объединить наблюдения за короткий период и за длительный период для получения оценок кривых как короткого, так и длительного периода [53]. Простую модель можно вывести следующим образом:
 (26)
(26)
 (26)
(26)
причем Ym = δ Z, где Ym - объем выпускаемой продукции, при котором средние затраты минимальны на кривой краткосрочных средних затрат, a Z - мера величины предприятия. Второй член в уравнении (26) относится к краткосрочным средним затратам для данного предприятия, в то время как третий член описывает вариацию стоимости предприятия. Одна из основных трудностей в использовании уравнения такого типа заключается в том, чтобы получить подходящую меру величины предприятия [53].
Теперь обратимся к результатам. Обычно считалось, что двумя главными выводами из эмпирических функций затрат были: первый, что кривая долгосрочных средних затрат имеет L-образную, а не U-образную форму, и второй, что краткосрочные предельные затраты постоянны. Критические замечания обычно были направлены против этих выводов, чтобы восстановить традиционные гипотезы. Критики приписывали возникновение смещений следующим причинам:
а) из-за бухгалтерских данных;
б) из-за статистической трактовки или обработки данных;
в) из-за ошибочной регрессии.
Доказывали, что эти смещения возникают из-за того, что кривая оцениваемых долгосрочных средних затрат не возрастает при высоких объемах выпуска и из-за линейности эмпирических кривых краткосрочных средних затрат.
Критики исследований затрат сразу указали на недостатки цифр, связанные с амортизацией [85]. Стеле утверждал, что бухгалтерское распределение амортизации приведет к ошибочной линейности. Но Джонстон прямо доказывает, что смещение появится, только если амортизация у пользователя действительно нелинейна относительно выпускаемой продукции. Например, если затраты пользователя резко возрастают для высоких уровней выпускаемой продукции, то оцененная кривая затрат будет более ровной, чем истинная кривая затрат.20
Статистическая оценка активов обычно основана на исторической стоимости. Следовательно, наклон функции долгосрочных затрат, вычисленных на множестве объектов, будет смещаться вниз, если большие фирмы имеют старое оборудование, а небольшие фирмы владеют новым оборудованием и зданиями.
Один из путей преодоления этой трудности - произвести пересчет стоимости всего оборудования в текущих ценах, но на практике нелегко осуществить такую переоценку, если у оборудования большой срок службы. Это смещение не столь важно для функций краткосрочных затрат, поскольку в измеряемую функцию должны быть включены только затраты пользователя капитала.
Третьим критическим замечанием является то, что теория краткосрочных затрат ограничена понятиями единичного экономического периода, в то время как учетные данные обычно собираются за более длительные периоды. Смит [80] возражал, что изменения затрат для экономических периодов будут усреднены в учетных данных, поэтому не стоит удивляться тому, что (учетные) предельные затраты будут почти постоянными. Для единичного экономического периода предельные затраты будут подниматься гораздо круче. Эта точка зрения была принята большинством критиков, но Джонстон [53] остроумно возражал, что использование данных за учетные периоды может существенно увеличить мощность обычного t-критерия при испытании гипотезы линейности. Он отметил, что даже тогда, когда объемы выпуска случайны, вполне возможно, что учетные данные будут играть большую роль при определении кривизны, чем данные единичного периода. Объяснение парадокса заключается в том факте, что Джонстон сравнивает данные для N единичных периодов с данными для N учетных периодов. Поскольку последние являются совокупностями первых, то N учетных периодов могут содержать столько же или больше информации, чем N экономических единичных периодов, в зависимости от их распределения во времени.
Основное критическое замечание в адрес статистической обработки заключается в том, что коррекция изменений цены фактора в исследованиях временных рядов для функций краткосрочных затрат увеличивает смещение в сторону линейности. Индексы Ласпейреса цен факторов в общем случае приведут к переоценке, увеличивая цены факторов, поскольку они никак не учитывают замещение. Дефляция с таким индексом с избытком компенсирует увеличение цены. Если высокие цены факторов связаны с высокими уровнями выпуска за период временного ряда, тогда для высоких значений выпуска продукции затраты будут снижаться. Можно обойти эту проблему, создавая другие виды индексов. Джонстон [53] показал, что при неправильно взвешенном индексе возможно смещение как в сторону линейности, так и в сторону криволинейности. Другой способ элиминировать изменение цен факторов заключается в том, чтобы заново оценить затраты на уровнях цен факторов в базисном периоде. Стеле [85], кажется, предполагает, что это сместит результаты в сторону линейности. Но Джонстон [53] утверждает, что, поскольку смещение не является отрицательным, этот метод, допускающий изменения цен фактора, будет способствовать сдвигу полученных результатов не к линейности, а к криволинейности. Это утверждение правильно, только если выпуск за базисный период находится где-то в середине распределения объемов выпуска. Но если объем выпуска за базисный период высок и находится на возрастающей части кривой краткосрочных средних затрат, и если все другие наблюдавшиеся объемы выпуска находятся ниже уровня базисного периода, смещение может быть в сторону линейности. Подобно этому, если объем выпуска за базисный период находится на снижающейся части кривой средних затрат, а все другие объемы выпуска находятся выше, смещение может быть линейным. Снова точный результат зависит в основном от выбора базисного периода.21
Во всяком случае чувствуется, что любое смещение статистических функций затрат, вносимое любыми методами дефляции, весьма мало по сравнению с искажениями из-за других факторов.
При изучении литературы оказывается, что "ошибка регрессии" вызывает самую сильную критику метода анализа по множеству объектов. Спорят, что производимая (и продаваемая) каждой фирмой продукция обычно является случайной переменной и колебания выпускаемой продукции вокруг среднего значения не контролируются фирмой. Фирма определит наилучший способ распределения выпускаемой продукции. По словам Фридмена, если нет переменных затрат, то исследование на множестве объектов продемонстрирует резкое снижение средних затрат. Когда фирмы классифицируются по действительному выпуску продукции, тогда возникает именно такой тип смещения. Фирмы с наивысшими объемами выпуска вряд ли будут производить продукцию на непривычно низком уровне; в среднем они явно скорее будут выпускать продукцию на необычно высоком уровне в отличие от тех, чей уровень выпуска является самым низким [39]. Эта критика была широко принята. Были предприняты попытки избежать ошибки регрессии путем классификации фирм по предприятиям и проверкой значимости внутризаводской и межзаводской регрессии [II]. С другой стороны, спорили, что если выпускаемая продукция является случайной переменной, то оценочной кривой затрат для принятия решения будет кривая ожидаемых затрат, а не кривая затрат, вызываемых случайными изменениями объемов выпуска [94]. Кривые ожидаемых затрат будут более пологими, чем исходные кривые. Поскольку учетный период обычно включает в себя много единичных экономических периодов, имеющиеся реально в наличии данные в основном будут приближаться к ожидаемому объему выпуска. Если данное положение справедливо, то это дает начало объяснению того, почему в оцененных кривых затрат наблюдается почти линейность и почему следует более серьезно воспринимать результаты этих исследований.
В табл. 1-3 собраны разнообразные, хотя и не исчерпывающие результаты по исследованию затрат. К сожалению, невозможно учесть все ограничения в каждом исследовании и точно объяснить их влияние на эти результаты. Остается только надеяться, что краткое описание результатов в последней графе не слишком искажает выводы авторов. Тип данных указан в третьей графе; данные опросов обозначены буквой Q, инженерные данные - Е, тогда как TS и CS описывают исследования временных рядов и совокупностей объектов соответственно. В графе "Период" указано, относится ли объект исследования к кривым краткосрочных (S) или долгосрочных (L) затрат.
Одной из примечательных сторон этих таблиц является преобладание исследований сферы коммунальных предприятий и железных дорог. Вероятно, это происходит благодаря наличию данных для национализированных или регулируемых отраслей. Эти отрасли имеют снижающиеся или постоянные долгосрочные средние затраты, за исключением восточных железных дорог в США [11]. Немногие исследователи кривых краткосрочных затрат сферы коммунальных предприятий выдвигают предположение, что краткосрочные средние затраты уменьшаются до уровня полного использования производственной мощности и что за пределами наблюдавшихся объемов выпуска предельные затраты постоянны. Эти результаты не опровергают того, что говорит традиционная теория о форме функции затрат. Коммунальные услуги и естественные монополии всегда рассматривались как исключение из привычной гипотезы об U-образной форме кривых затрат. И формы кривых, появляющиеся в эмпирических работах, подобны графикам, которые изображаются на аудиторных досках.
Таблица 1
Результаты исследований кривых затрат
Общие отраслевые исследования
| Автор | Отрасль | Тип | Период | Результат |
| Бэйн [8] | Обрабатывающая промышленность | Q | L | Небольшая эконо- мия от масштаба многозаводских фирм |
| Эйтман, Гугри [32] | То же | Q | S | Предельные за- траты ниже средних затрат при всех объемах выпуска ниже "производствен- ной мощности" |
| Холл и Хитч [41] | " " | Q | S | В основном пре- дельные затраты уменьшаются |
| Лестер [58] | " " | Q | S | Уменьшающиеся средние перемен- ные затраты до производственной мощности |
| Мур [70] | " " | Е | L | Экономия от масштаба вообще |
| [91] | Разные отрасли промышленности | CS | L | Небольшие или средние заводы обычно имеют самые низкие затраты. Блэр [9] делает другие выводы |
Таблица 2
Результаты исследований кривых затрат
Отраслевые исследования
| Автор | Отрасль | Тип | Период | Результат |
| Альперт [2] | Металло- обработка | Е | L | Экономия от мас- штаба до 80000 фунтов в месяц, затем постоянная отдача |
| Джонстон [53] | Различная продукция | TS | S | "Прямые" затраты линейно зависят от объема выпус- ка. Предельные затраты постоян- ны |
| Дин [23] | Мебель | TS | S | Предельные зат- раты постоянны. Краткосрочные средние затраты "не смогли воз- расти" |
| Дин [24] | Кожаные ремни | TS | S | Значительно воз- растающие пре- дельные затраты. Дин отказался от их изучения |
| Дин [25] | Трикотаж | TS | S | Предельные зат- раты постоянны. Краткосрочные средние затраты "не смогли воз- расти" |
| Дин [26] | Универсальные магазины | TS | S | Предельные зат- раты падают или постоянны |
| Дин, Джеймс[27] | Обувные магазины | CS | L | Долгосрочные средние затраты характеризуются U-образной кри- вой (интерприти- руются не как возникающие из-за неэкономич- ности от масшта- ба) |
| Холтон [45] | Розничная торговля (Пуэрто-Рико) | E | L | Долгосрочные средние затраты характеризуются L-образной кри- вой. Но Холтон утверждает, что расходы на управ- ление могут недооцениваться при высоких объемах выпуска |
| Эзекиэль, Уайли [33,34] | Сталь | TS | S | Предельные зат- раты падают, но большие нормаль- ные погрешности |
| Интема [98] | " | TS | S | Предельные за- траты постоянны |
| Эрке [30] | Цемент | TS | S | Эрке считает пре- дельные затраты постоянными. Апель [4] утверждает, что предельные за- траты возрастают |
| Нордин [76] | Электростанция | TS | S | Предельные затраты возрастают |
Таблица 3
Результаты исследований кривых затрат
Коммунальные предприятия
| Автор | Отрасль | Тип | Результат |
| Ломакс[60] | Газ (Великобритания) | CS | Долгосрочные средние затраты снижаются (нет анализа распределения) |
| Гриббин[40] | То же | CS | Тоже |
| Ломакс [61] | Электроэнергия (Великобритания) | CS | " " |
| Джонстон [53] | То же | CS | " " |
| " | " " | TS | Краткосрочные средние затраты падают, затем выравниваются,стремясь к постоянным предельным затратам на уровне производственной мощности |
| Мак-Налти [66] | Электроэнергия (США) | CS | Средние затраты на управление постоянны |
| Нерлов [75] | То же | CS | Долгосрочные средние затраты, за исключением затрат на транспортировку, возрастают |
| Джонстон [53] | Уголь(Великобритания) | CS | Широкий разброс затрат на тонну |
| " | Пассажирский автотранспорт (Великобритания) | CS | Долгосрочные средние затраты либо падают, либо постоянны |
| " | Пассажирский автотранспорт (Великобритания) | TS | Краткосрочные средние затраты уменьшаются |
| Джонстон [53] | Страхование жизни (Великобритания) | CS | Долгосрочные средние затраты падают |
| Бортc [10] | Железные дороги (США) | CS | Долгосрочные средние затраты либо постоянны, либо падают |
| Бортc [11] | То же | CS | Долгосрочные средние затраты возрастают на Востоке, падают на Юге и Западе |
| Бростер [12] | Железные дороги (Великобритания) | TS | Затраты производства на единицу продукции падают |
| Мансфильд, Уэйн [62] | То же | Е | Предельные затраты постоянны |
Предмет спора заключается в определении постоянных предельных затрат по отрасли промышленности в табл. 2. Единодушного мнения нет, трактовка Апелем [4] результатов Эрке [80], Нордина [76] и, возможно. Дина [24] представляет собой исключение. Нетрудно понять, почему Интема и Эзекиэль и Уайли [84, 98] получили снижающиеся или постоянные предельные затраты. Почти все наблюдения были для уровней выпуска, находящихся намного ниже "производственной мощности" заводов;
результаты регрессии явно справедливы только для этих объемов выпуска, находящихся ниже производственной мощности. Тогда остаются три исследования Дина (мебель, трикотаж, универсальные магазины) и исследование Джонстона в пищевой промышленности, которые требуют объяснения.22 Однако очевидно даже на этой стадии, что свидетельства в пользу постоянных предельных затрат не непреодолимы. Конечно, пересмотр теории с целью включения этого явления не есть дело первостепенной важности.
Свидетельства в пользу существования экономии от масштаба производства, т. е. того, что долгосрочные средние затраты падают при увеличении выпуска продукции, снова четко установлены только для коммунальных предприятий. Кроме опросов и инженерных данных единственным исследованием долгосрочных затрат в промышленности является подсчет затрат в обувных магазинах, проведенный Дином и Джеймсом. Они вывели U-образную форму кривых затрат, но утверждали, что она была в основном за счет худших факторов, которые фирма должна была покупать по тем же ценам, а не за счет неэкономичности от масштаба производства. Изучение анкет методологически подозрительно, и на их выводы нельзя особенно полагаться.23 Исследования, основанные на инженерных данных, тоже неудовлетворительны, поскольку они оценивают только взаимоотношения между затратами на капитал и "производственной мощностью" оборудования. Неизвестно, что происходит с другими затратами (например, с административными), когда производственная мощность возрастает; они могут перекрыть возрастающую отдачу, которую должен бы получить завод.24 Эмпирические результаты ясно показывают, что коммунальным предприятиям и железным дорогам присущи снижающиеся (или по крайней мере постоянные) долгосрочные средние затраты, как это давно предсказывали экономисты. Для этих отраслей промышленности установленная теория никоим образом не опровергается. С другой стороны, для "конкурентных" отраслей промышленности гипотеза об U-образной форме кривых не внушает особого доверия, но не потому, что она опровергается прямыми эмпирическими доказательствами. Напротив, отсутствие уверенности вызвано очень малыми возможностями получить основание для прямого опровержения теории. Вместо этого мы имеем непрямые, косвенные доказательства. Но по крайней мере нет достаточного объема данных, которые убедительно опровергали бы гипотезу об U-образной форме кривой долгосрочных затрат и те плодотворные результаты, которые следуют из нее.
Литература
1. Alchian A. Costs and Outputs // The Allocation of Economic Resources / Ed. by M. Abramovitz et al. Stanford, 1959. (См. настоящее издание. - Прим. ред.).
2. Alpert S. В. Economy of Scale in the Metal Removal Industry // Journ. Industr. Econ. 1959. Vol. 17.
3. Andrews P. W. S. Manufacturing Business. London, 1949.
4. Apel H. Marginal Cost Constancy and its Implications // Amer. Econ. Rev. 1948. Vol. 38.
5. Arrow К. J. Capital-Labor Substitution and Economic Efficiency //Rev. Econ. a. Stat. 1961. Vol. 43.
6. Arrow К. J. The Economic Implications of Learning by Doing // Rev. Econ. Stud. 1962. Vol. 29.
7. Asher H. Cost-Quantity Relationships in the Airframe Industry // Rand Corporation. 1956. R291.
8. Bain J. S. Barriers to New Competition. Cambridge (Mass.), 1956.
9. Blair J. M. The Relation between Size and Efficiency of Business // Rev. Econ. a. Stat. 1942. Vol. 24.
10. Boris G. H. Production Relations in the Railway Industry // Econo-metrica. 1952. Vol. 20.
11. Boris G. H. The Estimation of Rail Cost Functions // Ibid. 1960. Vol. 28.
12. Broster E. J. Variability of Railway Operating Costs // Econ. Journ. 1938. Vol. 48.
13. Brown M., De Cani J. S. Technological Change and Distribution of Income. 1962. (Ms.).
14. Brown W. G., Arscott G. H. A Method for Dealing with Time in Determining Optimum Factor Inputs//Journ. Farm. Econ., 1958. Vol.40.
15. Charnes A., Cooper W. WL Mellon B. A Model for Optimizing Production by Reference to Cost Surrogates // Econometrica. 1955. Vol. 23.
16. Chenery H. B. Engineering Production Functions // Quart. Journ. Econ. 1949. Vol. 63.
17. Chenery H. B. Process and Production Functions from Engineering Data // Studies in the Structure of the American Economy / Ed. by W. Leontief. Oxford, 1953. Ch. 8.
18. Chisholm M. Economies of Scale in Road Goods Transport // Oxf. Econ. Papers. 1959. Vol. 11.
19. Coase R. H. The Nature of the Firm // Economica. N. S. 1937. Vol. 4. Nov. (См. настоящее издание. - Прим. ред.).
20. Cobb С. W. Production in Massachusetts Manufacturing 1890-1928 // Journ. Polit. Econ. 1930. Vol. 38.
21. Cobb С. W.* Douglas P. H. A Theory of Production // Amer. Econ. Rev. 1928. Vol. 18. (SuppL).
22. Daly P., Olsen E., Douglas P. H. The Production Function for Manufacturing in the U.S. 1904 // Journ. Polit. Econ. 1943. Vol. 51.
23. Dean J. Statistical Determination of Cost with Special Reference to Marginal Cost // Studies in Business Administration. Chicago, 1936. Vol. 7.
24. Dean J. Relation of Cost to Output for a Leather Belt Shop // Nat. Burean Econ. Res. Tech. Paper. 1941, N 2.
25. Dean J. Statistical Cost Functions of a Hosiery Mill // Studies in Business Administration. Chicago, 1941. Vol. 14.
26. Dean J. Dept. Store Cost Functions // Studies in Mathematical Economics and Econometrics / Ed. by 0. Lange. Chicago, 1942.
27. Dean J., James R. W. The Long-run Behavior of Costs in a Chain of Shoe Stores // Studies in Business Administration. Chicago, 1942. Vol. 15.
28. Dorfman R. Application of Linear Programming to the Theory of the Firm. Berkeley, 1951.
29. Dorfman R., Samuelson P. A; Solow R. Linear Programming and Economic Analysis. New York, 1958. 80. Ehrke К. Die Uberzeugung in der Zementindustrie, 1858-1918. Jena, 1933.
31. Eiteman W. J. Factors Determining the Location of the Least-Cost Point // Amer. Econ. Rev. 1947. Vol. 37.
32. Eiteman W. J., Guthrie G. E. The Shape of the Average Cost Curve // Ibid. 1952. Vol. 42.
33. Ezekiel M., Wylie K. H. Cost Curves for Steel Production // Journ. Polit. Econ. 1940. Vol. 48.
34. Ezekiel M., Wylie K. H. Cost Functions for the Steel Industry // Journ. Amer. Statist. Assoc. 1941. Vol. 36.
35. Ferguson A. R. Empirical Determination of a Multidimensional Marginal Cost Function // Econometrica. 1950. Vol. 18.
36. Ferguson A. R. Commercial Air Transportation in the United States // Studies in the Structure of the American Economy / Ed. by W. Leontief. Oxford, 1953. Ch. 11.
37. Florence P. S. The Logic of British and American Industry. London, 1953 (русский перевод: Флоренс С. Структура промышленности и управление предприятиями Британии и США. M., 1958. - Прим. ред.).
38. Friedman M. Essays in Positive Economics. Chicago, 1935.
39. Friedman M. Comment // Conference on Business Concentration and Price Policy. Princeton, 1955.
40. Gribbin Т. К. Production Costs in the Gas Industry // Oxf. Econ. Papers. 1953. Vol. 5.
41. Hall R. L., Hitch C. J. Price Theory and Business Behavior // Ibid. 1939, Vol. 2.
42. Heady E. 0., Dillon J. L. Agricultural Production Functions. Ames, 1962 (русский перевод: Хеди 9L Диллон Д. Производственные функции в сельском хозяйстве. М., 1965. - Прим. ред.).
43. Hirsch W. Z. Manufacturing Process Functions // Rev. Econ. a. Statist. 1952. Vol. 34.
44. Hirsch W. Z. Firm Progress Ratios // Econometrica. 1986. Vol. 24.
45. Holton R. H. On the Measurement of Excess Capacity in Retailing // Rev. Econ. Stud. 1956-1957. Vol. 24.
46. Houthakker H. The Pareto Distribution and the Cobb-Douglas Production Function in Activity Analysis // Ibid. Vol. 23.
47. Johansen L. Substitution Versus Fixed Production Coefficients in the Theory of Economic Growth: a Synthesis // Econometrica. 1959. Vol. 27.
48. Johnston J. Statistical Cost Functions in Electricity Supply // Oxf. Econ. Papers. N.S. 1952. Vol. 4.
49. Johnston J. Cost-Output Variations in a Multiple Product Firm // Manch. School. 1953. Vol. 21.
50. Johnston J. Labour Productivity and Size of Establishment // Bull. Oxf. Inst. Statist. 1954. Vol. 16.
51. Johnston J. Scale, Costs and Profitability in Road Passenger Transport // Journ. Industr. Econ. 1956. Vol. 5.
52. Johnston J. Statistical Cost Functions : A Reappraisal // Rev. Econ. a. Statist. 1958. Vol. 40.
53. Johnston J. Statistical Cost Functions. New York, 1960.
54. Kaldor N. The Equilibrium of the Firm // Econ. Journ. 1934. Vol. 44.
55. Klein L. R. Macroeconomlcs and the Theory of Rational Behavior // Econometrica. 1946. Vol. 14.
56. Klein L. R. An Introduction to Econometrics. London, 1962.
57. Koopmans Т. С. Three Essays on the State of Economic Science. McGraw-Hill',. 1957.
58. Lester R. A. Shortcomings of Marginal Analysis for Wage-Employment Problems // Amer. Econ. Rev. 1946. Vol. 36.
59. Lomax К. S. An Agricultural Production Function for the U.K., 1924-1947 // Manch. School. 1949. Vol. 17.
60. Lomax К. S. Cost Curves for Gas Supply // Bull. Oxf. Inst. Statist. 1951. Vol.13.
61. Lomax К. S. Cost Curves for Electricity Generation // Economica. 1952. Vol. 19.
62. Mansfield EL Wein H. Regression Control Charts for Costs // App. Statist. 1958. Vol. 7.
63. Markowitz H. Process Analysis of the Metal Working Industries // RAND Corporation. 1953. RM-1085.
64. Markowits H. Industry-wide, Multi-industry, and Economy-wide Process Analysis // The Structural Interdependence of the Economy. London, 1963.
65. Marschak J., Andrews W. H. Random Simultaneous Equations and the Theory of Production // Econometrica. 1944. Vol. 12.
66. McNulty J. Administrative Costs and Scale of Operations in the U.S. Electricity Power Industry // Journ. Industr. Econ. 1956. Vol. 5.
67. Monger К. The Laws of Return : A Study in Meta-Economics. New York, 1945.
68. Meyer J. R., Peck M. J., Stenason J., Zwick C. The Economies of Competition in the Transportation Industries. Harvard, 1959.
69. Minnas В. S. The Homohypallagic Production Function, Factor Intensity Reversals and the Hecksher-Ohiin Theorem // Journ. Polit. Econ. 1962. Vol. 70.
70. Moore F. T. Economies of Scale: Some Statistical Evidence // Qurt. Journ. Econ. 1959. Vol. 73.
71. Mukerji V. The CES or 'SMAC' Production-Function When There Are More Than Two Inputs // Discussion Paper 32. Univ. of Birmingham. 1962.
72. Mundlak Y. Estimation of Production Functions from a Combination of Cross Section and Time Series Data // Read at Meeting of Econometric Society. New York, 1961. (Mimeograph).
73. NatafA. Sur la Possibilite de Construction de certains Macromodeles // Econometrica. 1950. Vol. 16.
74. Nerlove M. Notes on the Identification and Estimation of the Cobb- Douglas Production Function. Stanford, 1959. (Mimeograph).
75. Nerlove M. Return to Scale in Electricity Supply : Tech. Rep. 96. Stanford, 1961.
76. Nordin J. A. Note on a Light Plant's Cost Curves // Econometrica. 1947. Vol. 15.
77. Robinson E. A. G. The Structure of Competitive Industry. Cambridge, 1935.
78. Sargan J. D. Estimation of Economic Relationships Using Instrumental Variables // Econometrica. 1958. Vol. 26.
79. Simkin С. G. F. Aggregate Production Function // Econ. Record. 1955. Vol. 31.
80. Smith С. A. The Cost Output Relation for the U. S. Steel Corporation // Rev. Econ. a. Statist. 1942. Vol. 24.
81. Smith V. L. Investment and Production. Cambridge, 1961.
82. Solow R. M. The Production Function and the Theory of Capital // Rev.
Econ. Stud. 1955-1956. Vol. 23.
83. Solow R. M. Technological Change and the Aggregate Production Function // Rev. Econ. a. Statist. 1957. Vol. 39.
84. Solow R. M. Substitution and Fixed Proportions in the Theory of Capital // Rew. Econ. Stud. 1962. Vol. 29.
85. Staehle H. The Measurement of Statistical Cost Functions. An Appraisal of Recent Contributions // Amer. Econ. Rev. 1942. Vol. 32.
86. Stigler G. J. Production and Distribution in the Short-run // Journ. Polit. Econ. 1939. Vol. 47.
87. Stigler G. J. Production and Distribution Theories. New York, 1946.
88. Stigler G. J. Professor Lester and the Marginalists // Amer. Econ. Rev. 1947. Vol. 37.
89. Stigler G. J. The Theory of Price. Rev. edn. New York, 1952.
90. Stigler G. J. Economies of Scale // Journ. Law a. Economics. 1958. Vol. 1. Oct.
91. Temporary National Economic Committee // The Relative Efficiency of Large, Medium-sized and Small Business. Washington, 1941. Mon. 13.
92. Theil H. Linear Aggregation of Economic Relations. Amsterdam, 1954.
93. Verhulst M. J. Pure Theory of Production Applied to the French Gas Industry // Econometrica. 1948. Vol. 16.
94. Walters A. A. Expectations and the Regression Fallacy in Estimating Cost Functions // Rev. Econ. a. Statist. 1960. Vol. 42.
95. Walters A. A. Economies of Scale in Road Haulage : A Comment // Oxf. Econ. Papers. 1961. Vol. 13.
96. Whitin Т. M.. Preston M. H. Random Variations, Risk and Returns to Scale // Quart. Journ. Econ. 1954. Vol. 68.
97. Wiles P. J. B. A Rejoinder to Mr. Edwards // Econ. Journ. 1954. Vol. 64.
98. Yntema Т. 6. Steel Prices, Volume and Costs // Temp. Nat. Econ. Comm. Papers. 1940. Vol. 1.
ПРИМЕЧАНИЯ:
i Опубликовано в журнале "Econometrica" (1963. Vol. 31, N 1. Jan.-Apr.). Печатается по этому изданию с сокращениями.
1 Строго говоря, требуются еще два постулата: один устанавливает, что начало координат входит в производственное множество; другой утверждает, что существует точка, в которой выпуск хотя бы одного желаемого продукта имеет положительное значение [57, р. 78-82], а все промежуточные продукты используются полностью.
2 На "углах" предельная норма замены неоднозначна; она ограничена, однако, наклонами смежных отрезков.
3 Альтернативный подход заключается в том, чтобы отказаться от постоянства технологических законов и ввести для каждого предпринимателя свои базисные способы. Это могло бы быть полезным приемом в ряде случаев, но тогда теряется простота анализа.
4 В современной литературе ее называют функцией с постоянной эластичностью замещения, или CES-функцией. (Прим. ред.).
5 Формально мы можем учесть эти влияния на производственные функции предприятий путем включения совокупного продукта отрасли в производственную функцию i-й фирмы.
6 Внешние потери, вызванные фиксированным предложением фактора, входят в производственную функцию. Другие внешние потери возникают из-за того, что растут цены на ресурсы по мере увеличения объема выпуска. Эти денежные расходы не влияют на производственную функцию, но они изменяют кривые затрат.


