|
Для выявления названного выше различия можно ограничиться хозяйством с двумя взаимозаменяемыми благами (А и В). При повышении цены одного блага увеличивается спрос на другое и наоборот. Для изготовления этих благ применяются одни и те же факторы производства, поэтому по мере повышения цены одного блага производители уменьшают предложение другого и наоборот. В целях упрощения примем, что функции спроса и предложения на обоих рынках являются линейными:
| |
QAD = a - bPA + cPB; |
|
(8.1) |
| |
QAS = - k + mPA - lPB; |
|
(8.2) |
| |
QBD = f - gPB + hPA; |
|
(8.3) |
| |
QBS = - n + sPB - zPA, |
|
(8.4) |
где a,b,c,k,l,m,f,g,h,n,s,z - положительные коэффициенты, отражающие характер спроса и предложения.
Равновесная цена товара А находится из равенства
| |
a - bPA + cPB = - k + mPA - lPB  PA PA = 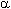 + 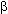 PB PB, |
|
(8.5) |
где 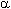  (a + k)/(m + b); (a + k)/(m + b); 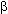  (c + l)/(m + b). (c + l)/(m + b).
Аналогично определяется равновесная цена товара В
| |
PB =  + 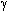 PB PB, |
|
(8.6) |
где   (f + n)/(g + s); (f + n)/(g + s); 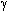  (h + z)/(g + s). (h + z)/(g + s).
Уравнения (8.5) и (8.6) определяют цены частичного равновесия, обеспечивающие равенство спроса и предложения на одном из рынков при заданной цене на другом рынке, на котором равновесия может и не быть.
Как следует из уравнений (8.5) и (8.6), между ценами благ, избранных для нашего анализа, существует положительная зависимость. Это объясняется тем, что с повышением цены на первое благо возрастает спрос на второе (кривая QD2 смещается вправо), в то же время производители уменьшают предложение относительно подешевевшего товара (происходит сдвиг кривой QS2 влево). То и другое ведет к повышению цены второго блага вслед за повышением цены первого.
 |
Рис. 8.1. Цены частичного
и общего равновесия
|
|
Равновесная система цен находится в результате совместного решения уравнений (8.5) и (8.6).
Различие между ценами частичного и общего равновесия показано на рис. 8.1, на котором уравнения (8.5) и (8.6) отображены прямыми линиями I и II. Каждая из них представляет множество цен частичного равновесия соответственно на рынках благ А и В.
Равновесная система цен определяется точкой пересечения прямых I и II. Они пересекутся, если параметры 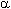 и и  в уравнениях (8.5) и (8.6) больше нуля, а в уравнениях (8.5) и (8.6) больше нуля, а 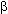 и и 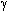 меньше 1. Экономически это означает, что спрос и предложение на каждом из рынков в большей степени зависят от цены блага, продающегося на данном рынке, чем от цены другого блага. В этих условиях общее равновесие является устойчивым. меньше 1. Экономически это означает, что спрос и предложение на каждом из рынков в большей степени зависят от цены блага, продающегося на данном рынке, чем от цены другого блага. В этих условиях общее равновесие является устойчивым.
|
Допустим, что на рынке блага А установилось равновесие при цене РА1. Линия I указывает на то, что в этом случае благо В продается по цене РВ1, которая не обеспечивает равновесия на своем рынке. При цене РА1 на рынке блага В равновесие обеспечивает цена РВ2 > РВ1. Следовательно, при сочетании РA1, РВ1 на рынке блага А существует равновесие, а на рынке блага В - дефицит. Когда цена блага В возрастет до РВ2, тогда на его рынке установится равновесие; но на рынке блага А теперь возник дефицит, так как при цене РВ2 для равновесия на нем нужна цена РA2 > РA1. Таким образом, в ситуациях, когда спрос и предложение на каждом из рынков в большей степени зависят от цены блага, продающегося на данном рынке, чем от цены другого блага, тогда система цен общего равновесия восстанавливается в результате взаимодействия спроса и предложения.
Если бы параметры функций спроса и предложения в системе уравнений (8.1) - (8.4) были таковы, что в уравнениях (8.5) и (8.6) 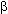 > 1, > 1, 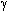 > 1, > 1, 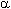 > 0, > 0,  > 0, то прямые I и II не пересеклись бы в квадранте I. Это означает, что не существует системы цен, обеспечивающих совместное равновесие на обоих рынках. > 0, то прямые I и II не пересеклись бы в квадранте I. Это означает, что не существует системы цен, обеспечивающих совместное равновесие на обоих рынках.
Если достижение совместного равновесия хотя бы только на двух рынках связано с выполнением целого ряда условий, то возможно ли существование общего экономического равновесия в экономике со множеством рынков благ и факторов производства? Для ответа на этот вопрос нужна модель, описывающая функционирование всего народного хозяйства. В ней кроме взаимодействия производителей и потребителей на рынках благ необходимо отразить взаимодействие между субъектами общественного хозяйства на рынках факторов производства, где формируются доходы потребителей, определяющие их спрос на блага. Если на рынках благ домашние хозяйства осуществляют расходы, а фирмы получают доходы, то на рынках факторов, наоборот, домашние хозяйства имеют доходы в виде заработной платы и дивидендов, а фирмы несут расходы по оплате труда и капитала.
 |
Рис. 8.3. Взаимодействие рынков благ
и факторов производства
|
|
С включением в модель рынков факторов производства экономика предстает в виде замкнутой системы, схематически представленной на рис. 8.3.
Первым экономистом, построившим такую модель для доказательства возможности существования общего экономического равновесия, был Л. Вальрас1. Рассмотрим эту модель в современном изложении.
|
|




